A lógica proposicional é baseada na lógica aristotélica (de primeira ordem) e faz uso de avaliações de verdadeiro e falso entre várias proposições, sem se importar com seus significados.

Dado um conjunto de símbolos de uma linguagem, chamado de alfabeto, definimos:

• Variáveis Proposicionais / Fórmulas atômicas: Elementos indivisíveis da lógica, representados por letras minúsculas: p, q, r, s,…
• Conectivos lógicos: Auxiliam na construção de novas fórmulas a partir das já existentes:
• ¬ negação (não)
• $\land$ conjunção (e)
• $\lor$ disjunção (ou)
• $\rightarrow$ implicação (se … então)
• $\leftrightarrow$ equivalência (se, e somente se)
• Delimitadores: São utilizados para evitar ambiguidades. Usamos os símbolos de parênteses ( ) .

Agora que temos um alfabeto, precisamos definir as regras gramaticais da linguagem, ou seja, como podemos construir fórmulas válidas com esses símbolos. Devemos seguir, em princípio, as seguintes regras:

1. Toda variável proposicional é uma fórmula;
2. A negação de uma fórmula também é uma fórmula (se A é fórmula, (¬A) também é);
3. Sejam A e B fórmulas. Aplicando os conectivos lógicos entre elas, temos outras fórmulas também: (A $\lor$ B) , (A $\land$ B), (A→B), (A $\leftrightarrow$ B);
4. As regras acima são as únicas geradoras de fórmula.

O cálculo de predicados é como uma extensão da lógica proposicional, onde adicionamos novos símbolos à linguagem previamente estabelecida:

• variáveis: $x,y,z$…
• constantes: $a, b, c$
• quantificadores: $\forall, \exists$
• símbolos de predicados: $P, Q, R, S,$…
• símbolos especiais: , (vírgula), = (igualdade), $P_i(x_j)$ (indexação de variáveis ou fórmulas)

As variáveis e constantes podem ser descritas em conjunto pelo nome “termo”. Variáveis representam objetos indefinidos enquanto as constantes objetos identificados. Os símbolos são utilizados para dar informações, relações e propriedades dos objetos.

Exemplo 1: Marta é animada : $A(m)$, onde $m$ identifica Marta e A a propriedade de ser animada.

Exemplo 2: Pedro gosta de Carla. $G(a,c)$, onde $G$ é o símbolo que representa a informação “gosta de”, $a$ representa Pedro e $c$ Carla.

Podemos generalizar a ideia para:

$P(x) :$ o objeto $x$ tem a propriedade $P$;

$(\forall x)P(x) :$ todo o x tem a propriedade P;

$(\exists x)P(x):$ existe pelo menos um x com a propriedade P.

De forma semelhante com o que fizemos com o cálculo proposicional, as seguintes são as regras para o cálculo de predicados:

1. Toda fórmula atômica é uma fórmula: Se T é um predicado e há n variáveis envolvidas, $T(t_1, t_2, ...,t_n)$ é uma fórmula atômica;
2. Se $\alpha,\beta$ são fórmulas, então também são fórmulas: $(\neg\alpha),(\alpha \lor \beta), (\alpha\rightarrow\beta), (\alpha \leftrightarrow \beta)$
3. Se $\alpha$ é uma fórmula e x uma variável, também são fórmulas: $(\forall x)\alpha, (\exists x)\alpha$
4. Somente as regras acima geram fórmulas.

Como dito anteriormente, a linguagem do cálculo proposicional é dada pelas fórmulas atômicas , dos parênteses para controle de hierarquia e dos conectivos. Entretanto, não há uso de quantificadores (disponíveis no cálculo de predicados).

Quando dizemos que a lógica é de primeira ordem, a estrutura inclui o cálculo proposicional, os quantificadores, as variáveis e constantes e os símbolos, ou seja, é o cálculo de predicados. Essa linguagem é utilizada na formalização da matemática. É dividida em três partes:

1. A linguagem, com seus símbolos e regras de boa formação de fórmulas;
2. A semântica, que análise o significado das proposições;
3. A axiomatização, ou sistema de axiomas, que são as regras para demonstração de teoremas.

Partindo de uma ou mais regras de inferências, ou seja, um conjunto de proposições (argumento) para se chegar a uma conclusão (valor), e determinados axiomas, um sistema dedutivo permite o uso destes aparatos para derivação de teoremas. Neste caso não há referência à semântica da linguagem, isto é, não se busca interpretação, mas consequência formal do que precede o resultado.

Quando temos uma fórmula que é sempre verdade independente da valoração avaliada, a chamamos de tautologia. Exemplo: $p \; \lor \; \neg p$ . Se $p$ é falso, não $p$ é verdadeiro, logo a fórmula é verdadeira. Se $p$ é verdadeira, não $p$ é falso, e temos resultado verdadeiro também.

No caso de $p\;\land\;\neg p$ temos o inverso, a fórmula é sempre falsa.

Existem outros casos onde a valoração implica em diferentes resultados, por exemplo, $p\rightarrow q$.

De acordo com essas observações podemos criar uma tabela de resultados, por exemplo com duas fórmulas atômicas, que é a tabela verdade.

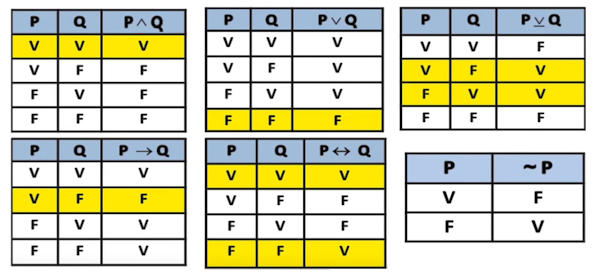
Sejam $A$ e $B$ fórmulas. Dizemos que $B$ é consequência lógica de $A$ se toda valoração de $A$ também satisfaz $B$, ou seja: $A\models B$.

Caso $B$ seja satisfeita por valorações que não satisfazem $A$, dizemos que $A$ implica logicamente $B$. Sejam $\Gamma$ um conjunto de fórmulas e $A$ uma fórmula, ambos em uma linguagem $L$. Se $A$ é consequência lógica de $\Gamma$, escrevemos: $\Gamma \models A$, de forma que todas as fórmulas de $\Gamma$ devem ser verdade simultaneamente com $A$.

A equivalência lógica entre duas fórmulas é dada quando as colunas de $A$ e $B$ na tabela verdade são idênticas, de forma que escrevemos:

$$ A\equiv B,\; se\; A\models B\;e\; B\models A $$

Um sistema tem a propriedade de corretude se dada uma propriedade do mesmo sistema, seus teoremas também possuem essa propriedade. O teorema da correção nos diz então que:

Sejam L uma linguagem de primeira ordem, $\Gamma$ um conjunto de fórmulas de L e A uma fórmula qualquer de L. Se $\Gamma \vdash A \Rightarrow \Gamma \models A$.

ou seja, o conjunto de fórmulas só pode deduzir o que é consequência (que modela) o sistema.

Teorema da dedução: Sejam $\Gamma$ um conjunto de fórmulas e A e B fórmulas, então

$$ \Gamma, A\models B \;sse \;\Gamma \models A\rightarrow B $$

Sejam uma linguagem de primeira ordem, $\Gamma$ um conjunto de fórmulas de $L$ e $A$ uma fórmula de $L$. Se $\Gamma \models A \Rightarrow \Gamma \vdash A$.

Neste caso, se A é consequência do conjunto de fórmulas, então A deve ser deduzível de $\Gamma.$ Isso implica que o sistema é completo.

O teorema da compacidade relaciona a consistência de todos os subconjuntos de um conjunto de fórmulas $\Gamma$ com a própria consistência de $\Gamma$. Consistência quer dizer, se ¬(x=x) não é consequência de $\Gamma$, então o conjunto dado é consistente.

Teorema: Seja $\Gamma$ um conjunto de fórmulas e suponha que todo subconjunto finito de $\Gamma$ é consistente. Logo, $\Gamma$ é consistente.

O teorema de Lowenhein-Skolem lida com a prova de resultados dos sistemas formais que estão sendo construídos. Esse teorema causou uma grande mudança na lógica matemática, tendo como expoentes dessa mudança de paradigma Hilbert, Post, Gödel e Tarski.

Suponha a seguinte sentença:

$\Phi : \forall x\exists y (y < x)$

O que essa relação nos diz, é verdadeira ou falsa? Isso depende do contexto, mas para a linguagem numérica, o conjunto dos inteiros por exemplo, para todo x existe um y que é menor do que ele. Entretanto, olhando para os números naturais, isso não é verdade, pois tomando x=0, a proposição é falsa.

Escrevendo na linguagem de modelos: $(\mathbb{Z}, <) \models\Phi$ e $(\mathbb{N}, <)\nvDash \Phi$.

Um dos problemas analisado pelo Skolem foi o de investigar se existe um conjunto $D$, enumerável, que é modelo para uma proposição que exige uma quantidade não enumerável de elementos. Parece óbvio que esse conjunto não existe, mas o teorema de Lowenhein-Skolem nos diz que na verdade isso é falso, o conjunto existe.

Enunciado do teorema: Se $L$ é uma linguagem e $B$ é uma L-estrutura de domínio infinito, então existe uma subestrutura elementar de $B$ cujo domínio é enumerável.

Como falamos antes, se $B$ é infinito e não enumerável, ter uma subestrutura enumerável é contraintuitivo e paradoxal.

Suponha um sistema lógico com um conjunto de fórmulas $\Gamma$ . O problema da decisão ocorre quando precisamos determinar um método efetivo que identifique que uma fórmula A pertence ao conjunto $\Gamma$ segundo as regras do sistema. Se o sistema é decidível podemos determinar quais são as fórmulas que são teoremas. No caso da lógica proposicional, a tabela verdade pode ser usada como método. No caso da lógica de primeira ordem isso não é verdade e isso segue na de segunda ordem.

É possível provar determinados teoremas matemáticos utilizando computadores? Essa é a área de prova automática de teoremas. Para avaliarmos as possibilidades de demonstração precisamos estabelecer o tipo de lógica. No caso da lógica proposicional, esse problema é decidível, porém não se sabe a complexidade em provas mais gerais. No caso da lógica de primeira ordem, entramos no problema avaliado por Gödel, eternizado em seu teorema de incompletude donde temos que eventualmente uma sentença verdadeira dentro do sistema não pode ser provada, fazendo com o que o algoritmo nunca termine.

Algumas são as lógicas não clássicas atualmente estudadas:

Lógica paraconsistente: Pode lidar com contradições, isto é, as regras do terceiro excluído e $p\;\land\neg p$ podem ser avaliados. O problema central é definir a consistência do sistema, de forma que seja possui construir proposições úteis com a sintaxe.

Lógica intuicionista: Tem como principal característica a implicação causal, gerando casos em que ambos $p$ e sua negação $\neg p$ sejam falsos.

Lógica fuzzy (difusa): É um tipo de lógica probabilística, onde o caráter verdade de uma proposição se encontra em um intervalo [0,1].

Referências:

1. Lógica Matemática - Rogério Augusto dos Santos Fajardo - EdUSP

< 4 - Geometria Analítica > 6 - Matemática Discreta