Iteração é um processo de repetição de um conjunto de operações com fins de resolver um problema. No caso de cálculo numérico, por exemplo, podemos iterar operações aritméticas em uma variável para obter uma solução mais refinada ou mais próxima de um determinado $\epsilon$ dado.

O método indutivo nos permite avaliar se uma determinada equação vale para um número k (caso base) o que acontece com k+1, ou seja, se essa propriedade continua valendo para qualquer outro m = k+1 > k.

Exemplo: Queremos demonstrar que $n+n=2\cdot n$

Para o caso base, $n=1$, temos que isso é verdade pois

$$ 1+1=2\cdot(1) $$

Nos casos de $n=2, n=3$, também temos sucesso, porém é inviável continuar avaliando os números dessa forma. Podemos olhar se a equação continua verdade quando utilizamos $k+1$, ou seja,

$$ n=k\\ k\rightarrow k+1\\ (k+1)+(k+1)=2\cdot(k+1) $$

queremos sair do caso inicial e chegar na equação anterior. Fazemos:

$$ k+k=2k\\ k+k+2=2k+2\\ k+1+k+1=2(k+1)\\ (k+1)+(k+1)=2(k+1) $$

De forma que provamos que vale para $k+1$.

O processo recursivo acontece quando temos uma função $f(x)$, com um caso base verdadeiro e onde podemos referenciar a mesma função para os outros casos $f(x+1).$ Por exemplo:

$$ f(0)=1\\ f(k+1)=2\cdot f(0) $$

De forma que de um caso base podemos retirar a informação dos outros. Por exemplo:

$$ n=0\\ f(0+1)=2\cdot f(0)=2(1)=2 \\ n=1 \\ f(1+1)=2\cdot f(1)=2(2)=4 $$

A regra geral então é:

• Testar o caso geral de $f(0)$
• O passo recursivo é testar a função em n+1 em termos da anterior $f(n), f(n-1),...$

Conjuntos não podem ser definidos sem referências circulares, mas podemos descrevê-lo basicamente como uma coleção de elementos que tem uma determinada propriedade. Algumas operações podem ser executadas em um conjunto qualquer como: união, intersecção, diferença, complemento, conjunto das partes, produto cartesiano e união disjunta.

Historicamente alguns problemas apareceram durante a formalização da teoria dos conjuntos, como o paradoxo de Russell. Uma forma visual de analisar as relações entre os conjuntos é chamada de diagrama de Venn.

Os conectivos lógicos estão relacionados de forma direta com as operações entre conjuntos:

• $\neg p \equiv\bar{A}$
• $p\;\lor\; q\equiv A\;\cup \;B$
• $p\;\land q \equiv A \cap B$

Também para relações, temos:

• $p\rightarrow q \equiv A\;\subseteq \;B$
• $p\leftrightarrow q \equiv A=B$

Operações não reversíveis (união, intersecção, diferença) não permitem identificar os conjuntos gerados do resultado. Operações reversíveis (complemento, conjunto das partes, produto cartesiano, união disjunta) é, obviamente, o inverso, partindo da operação e do conjunto(s) resultado podemos obter os conjuntos originais.

Dados os conjuntos A e B e o universal U:

União: $x\in A\;\cup\;B\Leftrightarrow x\in A \; \lor \;x\in \;B$

Intersecção: $x\in A\;\cap\;B\Leftrightarrow x\in A \; \land \;x\in \;B$

Diferença: $B-A=\{ x | x\in A\;\land\;x\in B \}=A\cap\bar{B}$

Complemento: $x\in \bar{A} \Leftrightarrow x\in A$ , onde $\bar{A}$ é o complemento de A.

Conjunto das partes: $\mathcal{P}(A)=\{X|X \subseteq A\}$, lembra que $\emptyset $ sempre pertence à A. Tamanho: $2^X$ .

Produto Cartesiano: $A\times B=\{\langle a,b \rangle\; |\; a\in A \;\land \;b\in B\}$

União disjunta: $A\cup^+B=\{ \langle a,0 \rangle \;|\;a\in A \} \; \cup \;\{ \langle b,1\rangle \;|\; b \in B\}$, não junta elementos com o mesmo “nome”.

Dados dois conjuntos A e B, um par ordenado é uma sequência de 2 objetos em ordem fixa:

$$ x\in A \; \land y\in B\\ \langle x,y \rangle\; ou\; (x,y)\\ \langle x,y \rangle\; \neq \langle y,x \rangle\; $$

Esse conceito pode ser generalizado para n objetos, uma n-upla:

$$ \langle x_1,x_2,x_3,...,x_n \rangle\\ (x_1,x_2,x_3,...,x_n) $$

Soma de pares ordenados: $\vec{x}=(x_1,x_2), \vec{y}=(y_1,y_2)$

$$ \vec{w}=\vec{x}+\vec{y}=(x_1+y_1,x_2+y_2) $$

Quando fazemos relações entre conjuntos ou elementos estamos criando regras de como tratar determinadas operações entre eles. Relações binárias, por exemplo, definem regras para dois elementos de cada vez. Isso é estendido para relações n-árias (3 ou mais elementos).

*Definimos*: Uma relação binário R de A em B é

$$ R \subseteq A\times B \; ou \; R:A\rightarrow B $$

R é um conjunto de pares. Dizemos também que $\langle a,b \rangle \in R$ ou $aRb$.

Endorrelação ocorre quando o conjunto domínio é igual ao contradomínio: $R:A\rightarrow A \; ou\; \langle A, R \rangle$.

Um diagrama de Venn pode ser utilizado para exemplificar as relações.

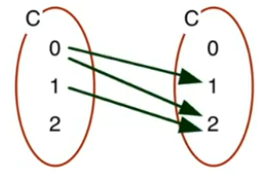
Também podemos utilizar um grafo para analisar uma determinada relação de um conjunto para ele mesmo. Toda endorrelação é um grafo, mas nem todo grafo é uma endorrelação. Para relações utilizados grafos dirigidos onde as arestas indicam um sentido. Seja $C=\{0,1,2\}$, o grafo para relação <, ou seja, $\langle C,< \rangle$

isso quer dizer 0 < 1, 0 < 2, 1 < 2.

Dados que os conjuntos envolvidos na relação binária são finitos, podemos representar $aRb$ como uma matriz $n*m$ se A tem n vetores e B m. Se $a_i$ se relaciona com $b_j$ então, na matriz, a linha i coluna j vai ter valor 1, do contrário, 0.

Matriz para a mesma relação vista no grafo anterior.

Podemos inverter a relação $aRb$ para $bRa$, que no caso da forma matricial, passamos a utilizar a matriz transposta.

Relação composta: $S\circ R=\{ \langle a,c \rangle\;|\; \exists \;b\in B(aRb\; \land \; bSc) \}$

Seja B um conjunto não vazio com as operações binárias + e * e a operação unária ‘, com dois elementos distintos 0 e 1. Se B respeitar as seguintes propriedades, é uma álgebra booleana:

1. $a+b=b+a;\quad a*b=b*a$
2. $a+(b*c)=(a+b)*(a+c);\quad a*(b+c)=(a*b)+(a*c)$
3. $a+0=a;\quad a*1=a$
4. $a+a'=1;\quad a*a'=0$

Também podemos escrever $\langle B,+,*,',0,1 \rangle$ .

Exemplo: $B=\{ 0,1\}$ . $1'=0, 0'=1$.

Se invertermos as operações + e *, assim como os elementos 0 e 1, obtemos novamente uma álgebra, onde esse procedimento é chamado de dual. O princípio da dualidade diz que o dual de qualquer teorema em álgebra booleana também é um teorema. Exemplo de dual:

$$ (1+a)*(b+0)=b \rightarrow (0*a)+(b+1)=b $$

Lei de DeMorgan: $(a+b)'=a'*b'; \quad (a*b)'=a'+b'$

Uma álgebra booleana é reticulado limitado, distributivo e complementar.

Teorema da representação: Se $x\neq 0 \in B$ e $B$ é uma álgebra booleana finita, com $a\in B$ um átomo, ou seja, $0\ll a$ , podemos escrever x de forma única, exceto pela ordem, de forma

$$ x=a_1+a_2+...+a_r $$

Se $P(A)$ é o conjunto de todos os subconjuntos do conjunto A de átomos, escrevemos $f:A\rightarrow P(A)$, isomorfismo :

$$ f(x)=\{ a_1, a_2, ...,a_r\} $$

O corolário nos diz que se uma álgebra booleana finita tem $2^n$ elementos, com n inteiro.

Seja K um conjunto de variáveis (letras ou símbolos) $K=\{k_1,k_2,...,k_n\}$. Uma expressão booleana E nessas variáveis é qualquer expressão criada com elas usando as operações +, * e ‘.

Exemplo: $E_1=(x+y'z)'+(xyz'+x'y)'$

Um literal é uma variável ou variável complementar x,x’,y,y’, etc… Um produto fundamental é um termo de um ou mais literais que não envolvem as mesmas variáveis: $xz', xy'z,x$, etc… Qualquer produto de literais pode ser avaliado como 0 ou um produto fundamental!

Exemplo 1: $xyx'z=x(yx')z=x(x'y)z=(xx')yz=0(yz)=0$

Exemplo 2: $xyzy=x(yz)y=x(zy)y=xz(yy)=xzy=x(zy)=x(yz)=xyz$

Uma expressão E é dita soma-de-produtos se E é um produto fundamental ou a soma de dois ou mais produtos fundamentais sem que um esteja contido em outro. Uma forma de soma-de-produtos de E é uma expressão booleana equivalente de uma expressão de soma-de-produto.

Podemos contar o número de literais envolvidos em cada termo e somar os totais para obter informações importantes das expressões. Por exemplo:

$$ E=xyz'+x'y't+xy'z't+x'yzt $$

O primeiro termo tem 3 literais, o segundo 3, o terceiro 4 e o quarto 4. Então $E_L=3+3+4+4=14$. Temos $E_s=4$ termos no total. Dizemos que uma expressão E é mais simples do que outra F se:

1. $E_L < F_L$ e $E_s\leq F_L$ ou
2. $E_L\leq F_L$ e $E_S < F_L$

Dizemos que E é mínimo se não há expressão do tipo somo-de-produtos mais simples do que E.

Seja E uma expressão booleana com n variáveis. A tabela verdade de E é dada por T(E), que também pode ser vista como uma função de $T:B^n\rightarrow B =\{ 0,1\}$, ou seja, em um circuito lógico, a cada n bits na expressão temos uma resposta dada por 0 ou 1.

Uma relação de ordem parcial é um subconjunto $R\subseteq A^2$, se e somente se: R é endorrelação reflexiva, antissimétrica e reflexiva. Caso isso seja verdade, A é dito conjunto parcialmente ordenado.

Diagramas de Hasse podem ser utilizados para visualizar as relações (grafo dirigido). Jamais temos ciclos nesses grafos.

Um exemplo interesse de relação de ordem é em um programa sequencial. Se há dependência causal de comandos $c_1;c_2;c_3$ , que é uma ordem parcial, ou seja

$$ \leq_c=\{ \langle c_1,c_2\rangle \langle c_1,c_3\rangle \langle c_2,c_3 \rangle \} $$

As relações de equivalência tem uma noção próxima de igualdade, mas utilizando formas diferentes. Equivalência deve ser reflexiva (o elemento x é igual a si mesmo). Transitividade (se a < b < c, a < c). Simetria (a=b, b=a).

*Definição*: $R\subseteq A^2$ é uma relação de equivalência se, e somente se, R é uma endorrelação reflexiva, simétrica e transitiva.

A relação de equivalência resulta em partições do conjunto em subconjuntos disjuntos e não-vazios, chamadas classes de equivalência. Toda partição induz uma relação de equivalência. Notação:

$$ A=\{A_1,A_2,...,A_n \}\\ A_i\;\cap\;A_j=\emptyset , i\neq j\\ \cup_{i=1}^nA_i=A\\ a_1\in A_1, a_2 \in A_2,...,a_n\in A_n $$

Exemplo: $\langle \mathbb{N},R_{mod2} \rangle=\{ \langle a,b \rangle \; |\; a\%2=b\%2 \}$. Divide os números naturais em duas partições: a) números pares; b) números ímpares.

Se dermos uma relação de equivalência, podemos encontrar todas as partições pelo conjunto quociente: $A\setminus R=\{ [a]_R\;|\; a\in A \}$ onde, $\forall a, [a]_R=\{ b\in A \;|\;aRb\}$

Se R é uma relação entre dois conjuntos A e B, dizemos que ela é:

funcional: $\forall a\in A, \forall b_1,b_2 \in B(aRb_1\land aRb_2\rightarrow b_1=b_2)$

injetora: $\forall a_1, a_2\in A, \forall b \in B(a_1Rb\land a+2Rb\rightarrow a_1=a_2)$

total: $\forall a\in A \; \exists \; b \in B(aRb)$

sobrejetora: $\forall b\in B \; \exists \; a \in A(aRb)$

isomorfismo: $\exists\; R^{-1}\subseteq B\times A\;(R ^{-1}\circ R=\imath_A\land R\circ R^{-1}=\imath_B)$

Uma função é uma relação funcional.

Reticulados (Lattices em inglês) são pares do tipo (S,R) onde S é um conjunto e R uma relação, com as seguintes propriedades:

1. $\forall x,y \in S, GLB(x,y)\neq \emptyset$
2. $\forall x,y \in S, LUB(x,y)\neq \emptyset$

onde GLB (greatest lower bound) ou ínfimo é o maior valor de limite inferior e LUB (lower upper bound) supremo é menor valor de limite superior. Dizemos que S é um tipo de conjunto ordenado se as propriedades são observadas (também chamado: partially ordered set, ordered set, poset). Os dois valores limites devem existir para S ser um reticulado. Usando um diagrama de Hasse podemos identificar se o conjunto é um reticulado ou não, encontrado os valores limites segundo quaisquer pares de pontos.

Exemplo 1: $(\mathbb{Z},\geq)$ . No conjunto dos inteiros, temos ordem total e um reticulado infinito.

Exemplo 2: $(S,\subseteq)$. Um conjunto de conjuntos com a operação de subconjunto é um conjunto parcialmente ordenado.

Se todos os elementos de S respeitam as propriedades de ordenação, então temos um conjunto totalmente ordenado.

Símbolo de ordenação: $a\succ b, b\prec a$

Se um conjunto S tem ambas as operações, $\succeq, \preceq$, chamamos de ordem dual.

Se A é subconjunto de S e $a,b \in A$ onde $a\preceq b$, dizemos que A tem ordem induzida e é um subconjunto ordenado.

Quase ordem: Quando um conjunto S respeita as propriedades irreflexivas e transitiva de ordem.

Dados $a,b\in S$ onde não ocorre de a preceder b ou b preceder a, temos elementos não comparáveis: $a\parallel b$.

Isomorfismo: Se $f$ é uma função injetiva $f:X\rightarrow Y$, dizemos que é isomórfica se ela preserva a ordem.

1. $a\preceq a'$ então $f(a)\preceq f(a')$
2. $a \parallel a'$ então $f(a)\parallel f(a')$

Um conjunto é dito bem ordenado se qualquer subconjunto seu tem um primeiro elemento.

Uma operação binária * é uma função $S\times S$ que podemos escrever como $*(a,b), a*b, ab$ .

Seja S um conjunto não vazio com uma operação associativa e um elemento neutro. S é chamado de monóide. Se o elemento neutro não existe, então S é um semigrupo.

Se G é um conjunto não vazio com uma operação binária, lei associativa, elemento identidade e inversos, então G é grupo.

Seja R um conjunto não vazio com duas operações binárias +, *. R é um anel se:

1. $a,b,c\in R \rightarrow (a+b)+c=a+(b+c)$
2. $\exists 0\in R\;|\; a+0=0+a, \forall a\in R$
3. $\forall a\in R,\exists-a\;|\; a+(-a)=(-a)+a=0$
4. $\forall a,b\in R\; a+b=b+a$
5. $\forall a,b,c \in R, (ab)c=a(bc)$
6. $\forall a,b,c\in R, i) \; a(b+c)=ab+bc; \; ii) (b+c)a=ba+ca$

A teoria dos códigos lida com problemas de transmissão de informação em canais com ruídos, ou seja, como aumentar a confiabilidade que o foi transmitido vai chegar corretamente ao receptor. Códigos de correção de erros são utilizados em diversos sistemas de comunicação, desde comunicação espacial até a qualidade de áudio e fones sem fio. Particularmente em computadores, onde utilizados dígitos binários, uma troca de dados tem bilhões de bits. O canal de transmissão possui ruído o que pode afetar os dados enviados. Desta forma é importante identificar se um erro aconteceu (error detection) e se é possível corrigí-lo (error correction).

O método principal para recuperar mensagens distorcidas é utilizar redundância. Em linguagens naturais podemos utilizar o contexto, interpretação e vocabulário para detectar e corrigir uma palavra escrita incorretamente em uma frase. Quando um sistema de tradução sugere uma palavra mais próxima da digitada incorretamente, dizemos que ele usa o princípio de maior similaridade. Por exemplo, ao escrever “seje feliz” o sistema vai indicar “seja feliz” como sugestão. Alguns softwares podem corrigir automaticamente as palavras na medida que o usuário vai digitando o texto. Porém, como aplicamos esse princípio quando lidamos com comunicação de computadores?

Vamos supor que para comunicar uma mensagem entre o computador A com o B, utilizamos 1 para sim e 0 para não. Mas como vamos saber que um erro aconteceu no caminho? Se A enviar 1 e B receber 0, como saber que 0 não era a mensagem? 0 e 1 são igualmente válidos e prováveis. Vamos assumir algumas características do modelo de comunicação, chamado BSC (binary symmetric channel):

1. Cada bit de transmissão tem a mesma probabilidade p de mudar (1 para 0 e 0 para 1). Se o bit $b_1$ tem probabilidade p, então o bit $b_2$ tem probabilidade 1-p. Chamamos 1-p de confiabilidade do BSC;
2. Erros acontecem de forma aleatória e independente.
3. Quebramos a mensagem original em blocos (por ex, 4 bits);

Um exemplo de redundância seria reenviar a mensagem novamente em sequência da mensagem original. Por exemplo: 1011**1011**, os quatro primeiro bits forma a mensagem original e os quatro último a redundância. Podemos compará-lo para verificar se aconteceu um erro. Esse tipo de modelo é chamado de código repetido simples. Quando usamos esse tipo de redundância, temos uma taxa de informação de 1/2, que é a razão entre a informação original e a repetição (cada bit nesse caso é repetido uma vez). Se tivermos 3 vezes, então a taxa é 1/3.

Outra forma de adicionar verificação é por verificação de paridade. Por exemplo, somamos todos os bits e adicionamos o resultado ao final da mensagem. Se queremos enviar 1011, então $s=1+0+1=1$, logo a mensagem final será 1011**1**. Também podemos calcular o módulo 2 da soma de todos os bits.

No caso do código de Hamming, adicionamos 3 novos bits de correção que estão relacionados com os bits originais da seguinte forma: Se $x_1,x_2,x_3,x_4$ são os bits originais, então, a mensagem final seria na forma $x_1x_2x_3x_4x_5x_6x_7$ onde

$$ x_5=x_1+x_2+x_4\\ x_6=x_1+x_3+x_4\\ x_7=x_2+x_3+x_4 $$

com as operações em módulo 2. A taxa nesse exemplo é dada por 4/7, 4 dos 7 bits originais são de validação.

A definição formal é dada pelo seguinte: Um código C de tamanho n sobre um alfabeto F é um subconjunto $F^n=F\times F \times ...\times F$ , ou seja , o produto cartesiano de F por si mesmo n vezes. Isso consiste de n-tuplas de elementos de F.

Chamamos os elementos de C de codewords, isso nos dá todas as palavras válidas da linguagem utilizada. O alfabeto mais importante é o binário: $B=\{0,1\}$. Chamamos um código sobre o alfabeto binário de código binário.

Se $C=\{ 1010, 0101, 1111 \}$ , onde $c_1=1010, c_2=0101, c_3 =1111$ e recebemos a mensagem $u=0100$ , como podemos saber que houve um erro? Como pode ser corrigido? Se levarmos em conta que $u$ parece com $c_2$ podemos criar uma função distância, ou distância de Hamming, para calcular o número de posições em que os vetores diferem.

$$ d(u,c_1)=3\\ d(u,c_2)=1\\ d(u,c_3)=3 $$

Aquele que tem menor distância tem maior chance de ser o valor intencionado. A distância mínima é dada por $min\{ d(u,v) : u,v\in C, u\neq v \}$. O peso mínimo $min\{ wt(u):u\in C,u\neq \emptyset \}$ onde $wt(u)=(u+v)$ é a soma (módulo 2) dos vetores. Nesse caso temos que $d(u,v)=wt(u+v)$.

Temos que $B^n$ sobre o corpo binário $B$ é um espaço vetorial e podemos utilizar todas as operações existentes neste tipo de conjunto. Um código binário linear é um subconjunto do espaço $B^n$. Para um código linear, a distância mínima é igual ao peso mínimo.

Podemos expressar os códigos como matrizes também, representando vetores. Uma matriz G geradora de código linear para o conjunto C é aquela que gera C. Dizemos $C=\{ u*G: u\in B^k \}$ ou $C=\{ u\in B^k: H*u=\emptyset \}$ onde H é matriz de verificação de paridade.

A teoria dos domínios é uma estrutura matemática para definir os valores e operações executadas neles em uma linguagem de programação. Operações em programas também são valores de dados, ou seja, ambos, operações e valores são domínios computacionais. Podemos representar qualquer configuração finita por símbolos (bitstring).

Uma ordem parcial é um par $\langle B, \sqsubseteq\rangle$ que consiste em:

1. Um conjunto B chamado de universo;
2. Uma operação binária $\sqsubseteq$ no conjunto B, chamada de ordenação aproximada, que é
1. reflexiva: $\forall a \in B\;[x\sqsubseteq x]$
2. antissimétrica: $\forall x, y\in B\; [x\sqsubseteq y] \; e\; [y\sqsubseteq x] \;$ implica $x=y$
3. transitivo: $\forall x,y,z \in B\; [x\sqsubseteq y] \; e\; [y\sqsubseteq z] \rightarrow x\sqsubseteq z$

Uma ordem parcial completa, cpo, é uma ordem parcial onde cada subconjunto tem pelo menos um limite superior em B.

Dada uma base com número finito de entradas em B, o domínio correspondente $\mathcal{D}_B$ é construído pela formação de todos os subconjuntos consistentes que são fechados pela operação $\sqsubseteq$ , ou seja, $S\subseteq B$ é um elemento de $\mathcal{D}_B$ se e somente se

1. $\forall s\in S, \forall b \in B, b\sqsubseteq s \Rightarrow b\in S$
2. $\forall r,s \in S r\sqcup s \in S$

onde $\sqcup$ é a operação $a \land b.$

Referências:

1. Schaum Outline of Discrete Mathematics - Seymour Lischutz, Marc Lipson
2. An introduction to Coding Theory via Hamming Codes - A Computational Science Model - Nuh Aydin
3. Domain Theory: An Introduction - Robert Cartwright, Rebecca Parsons

< 5 - Lógica Matemática > 7 - Probabilidade e Estatística