O princípio básico da computação gráfica é transformar dados em uma imagem, utilizando-se de técnicas para exibição de pixeis (picture element), que representam o menor elemento de uma imagem exibida em uma tela. Cada pixel só pode ter uma cor. No modelo RGB (red-green-blue, chamadas de cores primárias), a mistura das três cores em diferentes proporções gera um espectro de diferentes cores e pode ser programado com três números entre 0 e 255. Por exemplo:

$$ Branco\; =\;(255,255,255)\\ Preto\;=\;(0,0,0) $$

Pixeis (ou Pixels) podem ser codificados como matrizes para gerar imagens também, onde cada elemento da matriz aceita um bit. Se o valor for 1, equivale ao pixel preto, se 0, nada é exibido.

Imagens vetoriais são formadas por elementos geométricos euclidianos: pontos, curvas, linhas e polígonos. São utilizadas fórmulas para transformar, posicionar, mudar o tamanho e a forma do objeto.

A técnica de rasterização transforma uma imagem vetorial em matricial (converte elementos geométricos em linhas e colunas de 0 ou 1). Essa transformação pode gerar problemas como o serrilhado (aliasing).

As transformações geométricas básicas primárias são:

• Translação: desloca pontos por uma distância e direção fixas;
• Rotação: desloca pontos ao redor de um eixo;
• Escala: desloca pontos para alterar o tamanho, mas que pode deformar o objeto;

As secundárias:

• Reflexão
• Cisalhamento

Alguns elementos gráficos podem ser combinados para construir objetos mais complexos, eles são chamados de primitivos:

• 2D : ponto, linha, polilinha, polígono, elipse, arco;
• 3D : cubo, esfera, cilindro, cone, tubo.

Os vértices são o ponto de partida nas primitivas geométricas e são representados por quatro coordenadas: $(x,y,z,w)$. Isso ocorre por causa das coordenadas homogêneas, que é um sistema de coordenadas em geometria projetiva onde um ponto no espaço 2D é um projeção de um ponto 3D em um plano. O ponto possui três valores $(x_h,y_h,h)$ onde $h$ é o parâmetro homogêneo e diferente de zero. Normalmente é utilizado $h=1$ para manter as coordenadas Euclidianas e ter maior poder de representação.

Quando realizamos uma translação no plano estamos na verdade resolvendo o seguinte sistema:

$$ x'=x+t_x \\ y'=y+t_y $$

que em notação matricial pode ser escrito como $P'=P+T$ onde

$$ P=\begin{bmatrix} x \\ y \end{bmatrix} ,P'= \begin{bmatrix} x' \\ y' \end{bmatrix}, T=\begin{bmatrix} t_x \\ t_y\end{bmatrix} $$

onde podemos então gerar uma matriz de translação que vai atuar nas coordenadas $(x,y)$:

$$ \begin{bmatrix} x'_h \\ y_h' \\ h \end{bmatrix} = \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x_h \\ y_h \\ h \end{bmatrix} $$

Quando $h=1$ temos um caso particular das coordenadas homogêneas, que é o sistema cartesiano.

Da mesma forma, a transformação em escala pode ser executada através da seguinte operação $P'=S\cdot P$ ,

$$ \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix}= \begin{bmatrix} S_x & 0 & 0 \\ 0 & S_y & 0 \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} $$

onde $S_x$ e $S_y$ devem ser maiores do que zero com as seguintes consequências:

• Se $S_x > 1$ e $S_y > 1$ : objeto aumenta
• Se $S_x < 1$ e $S_y < 1$ : objeto diminui
• Se $S_x=S_y$ : escala é uniforme
• Se $S_x\neq S_y$ : escala é diferencial

No caso da rotação, consideramos o raio $r$, constante, o ângulo $\phi$, original, e o ângulo $\theta$ de rotação. Na forma matricial temos:

$$ \begin{bmatrix} x' \\ y' \end{bmatrix}= \begin{bmatrix} cos(\theta) & -sin(\theta) \\ sin(\theta) & cos(\theta) \end{bmatrix} \cdot \begin{bmatrix} x \\ y \end{bmatrix} $$

Em coordenadas homogêneas temos:

$$ \begin{bmatrix} x' \\ y' \\ '\end{bmatrix}= \begin{bmatrix} cos(\theta) & -sin(\theta) & 0 \\ sin(\theta) & cos(\theta) & 0 \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ 1\end{bmatrix} $$

A vantagem de usar coordenadas homogêneas é poder "juntar" as matrizes de transformação em apenas uma. Por exemplo: $P'=M_2\cdot M_1\cdot P=M\cdot P$, onde

$M=M_2\cdot M_1$.

Dado um ponto de referência $(X_f,Y_f)$ podemos transladar um objeto com relação a ele através da matriz:

$$ \begin{bmatrix} S_x & 0 & X_f(1-S_x) \\ 0 & S_y & Y_f(1-S_y) \\ 0 & 0 & 1 \end{bmatrix} $$

O mesmo pode ser feito para rotação, com a seguinte matriz:

$$ \begin{bmatrix} cos(\theta) & -sin(\theta) & X_r-X_rcos(\theta) +Y_rsin(\theta) \\ sin(\theta) & cos(\theta) & Y_r-Y_rcos(\theta)-X_rsin(\theta) \\ 0 & 0 & 1 \end{bmatrix} $$

A matriz de reflexão depende do eixo escolhido:

$$ Y = 0 : \begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{bmatrix}, X = 0 : \begin{bmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}, \\X = Y = 0 : \begin{bmatrix} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \end{bmatrix} $$

Cisalhamento é uma transformação que distorce um objeto (shearing) em uma direção:

$$ \begin{bmatrix} 1 & sh_x & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} $$

As transformações em 3D são feitas a partir das de 2D, porém incluindo a coordenada $z$ e utilizando matrizes $4\times4$. Para translação:

$$ \begin{bmatrix} x' \\ y' \\ z' \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} $$

Escala:

$$ \begin{bmatrix} x' \\ y' \\ z' \\ 1 \end{bmatrix} = \begin{bmatrix} S_x & 0 & 0 & 0 \\ 0 & S_y & 0 & 0 \\ 0 & 0 & S_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\cdot \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} $$

Rotação (para x):

$$ \begin{bmatrix} x' \\ y' \\ z' \\ 1 \end{bmatrix} = \begin{bmatrix} cos(\theta) & -sin(\theta) & 0 & 0 \\ sin(\theta) & cos(\theta) & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\cdot \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} $$

Uma janela de recorte é uma projeção de uma cena em 3D no plano de projeção.

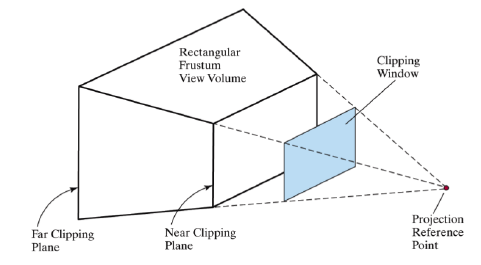
Os planos de recorte podem ser longe ou perto, perpendiculares ao eixo $z_{view}$. A porção visível do mundo é chamada de Frustum, tronco ou fatia seccionada de algum sólido geométrico.

O conceito de "viewport" desempenha um papel fundamental na área da computação gráfica, permitindo a exibição eficiente de imagens e gráficos em telas e dispositivos diversos. O termo "viewport" se refere à região retangular da tela onde o conteúdo gráfico é renderizado e exibido ao usuário. É uma janela através da qual observamos o mundo virtual criado por meio de algoritmos e representações digitais.

Projetar é o processo de converter pontos de um espaço d-dimensional em outro d-1-dimensional, ou seja, uma redução da dimensionalidade que pode ou não preservar certas relações do objeto original. Pontos em 3D podem ser projetados em um plano 2D. Pelo centro de projeção emanam raios de projeção, utilizados para intersectar o plano de projeção e gerar a imagem.

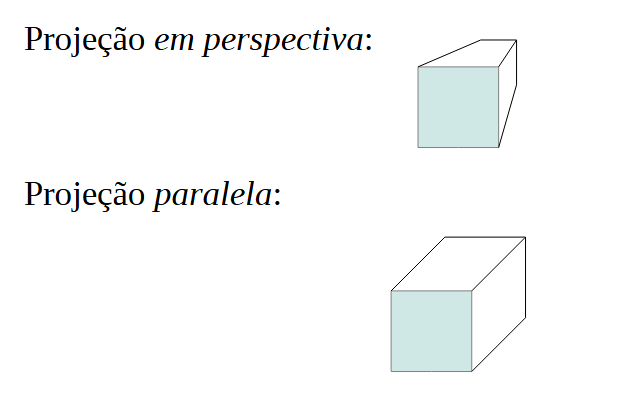
A projeção paralela é utilizada para exibir um objeto como se ele tivesse forma e tamanho aproximadamente reais. O centro de projeção está no infinito. Deve se especificar o vetor de direção da projeção.

Na projeção em perspectiva estamos visualizando um objeto de um ponto no sistema de coordenadas e o centro de projeção é um ponto do espaço que deve ser especificado. O objeto a ser exibido deve ser deformado proporcionalmente à distância do centro de projeção. Raios que saem do centro de projeção atravessam um plano de visualização (view plane).

Algumas variações da projeção pespectiva:

• Um Ponto de Fuga: Também conhecida como projeção cônica simples, nessa variação todas as linhas de projeção convergem para um único ponto de fuga no horizonte.
• Dois Pontos de Fuga: Aqui, as linhas de projeção são divididas em dois grupos que convergem para dois pontos de fuga no horizonte. Isso é frequentemente usado para representar objetos em ângulos diferentes.
• Três Pontos de Fuga (ou Projeção em Três Pontos): Esta variação é usada quando os objetos estão em um ângulo oblíquo em relação ao observador, como um edifício visto de cima.

Projeções paralelas podem ser divididas entre ortográfica e oblíqua. No primeiro, os raios de projeção são normais ao plano de projeção, enquanto na última não. Projeções ortográficas comuns são chamadas de vista frontal, lateral e superior.

As retas paralelas não são conservadas, exceto quando estão contidas em um plano paralelo ao de projeção, o mesmo ocorre para os ângulos. A projeção paralela preserva retas que são paralelas, enquanto os ângulos só são preservados em planos que estão paralelos ao de projeção.

Os pontos $x_p,y_p$ do plano de visualização pode ser escritos em função dos pontos de perspectiva $x_{prp}, y_{prp}, z_{prp}$:

$$ x_p=x(z_{prp}-z_{vp})+x_{prp}(z_{prp}-z_{vp})\\ y_p=y(z_{prp}-z_{vp})+y_{prp}(z_{prp}-_{vp}) $$

onde $(x,y)$ é um ponto qualquer no sistema mundo.

A matriz perspectiva é dada por $M_{normpers}=M_{xyscale}\cdot M_{pers}$ .

A projeção deve ser normalizada com relação à escala, levando em conta a janela de recorte:

• Diminuir ângulo: move ponto de projeção para longe e dá zoom in na cena;
• Aumentar ângulo: ponto de projeção movido para perto, zoom out da cena.

O volume de visão em projeção perspectiva refere-se ao espaço tridimensional que é capturado e visualizado em uma cena quando representada em uma imagem bidimensional usando a técnica de projeção perspectiva. Em outras palavras, é o intervalo de espaço que pode ser visto a partir de um determinado ponto de observação e que será projetado na imagem final.

Na projeção ortogonal há mapeamento de um vértice $(x,y,z)$ para $(x,y)$ e as coordenadas dentro do volume de visão já estão corretas no sistema de projeção. É paralela ao eixo $z_{view}$. É preciso normalizar o volume, dados os parâmetros $z_{near}, z_{far}$ e a janela de corte. A matriz necessário é:

$$ M_{ortho,norm}=\begin{bmatrix} \frac{2}{xw_{max}-xw{min}} & 0 & 0 & \frac{xw_{max}+xw_{min}}{xw_{max}-xw{min}} \\ 0 & \frac{2}{xw_{max}-xw{min}} & 0 & -\frac{xw_{max}+xw_{min}}{xw_{max}-xw{min}} \\ 0 & 0 & \frac{2}{xw_{max}-xw{min}} & \frac{z_{near}+z_{far}}{z_{near}-z_{far}} \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} $$

Algumas anomalias ocorrem na projeção perspectiva:

• Encurtamento: Objeto parece menor quando se aumenta a distância do centro de projeção.
• Pontos de fuga: Dão a ilusão de interseção entre um conjunto de retas paraleas.

Uma câmera é um dispositivo ótico que recebe e desvia os raios de luz. As câmeras podem ser reais ou virtuais. Uma câmera real é como uma câmera fotográfica, a imagem é invertida ao passar por uma lente, que é um sistema óptico, e o encontro dos raios de luz forma a projeção do objeto. As imagens virtuais, por outro lado, são geradas por espalhamento dos raios e dizemos que tem seu cruzamento em um ponto inacessível do sistema de óptico, sendo que a imagem não pode ser projetada e tem a mesma orientação do objeto. A câmera virtual simula esse comportamento através de modelos matemáticos. Esse é o tópico de projeções de imagens, regido pela geometria projetiva.

Podemos caracterizar uma câmera de forma matemática por parâmetros:

• intrínsecos: internos da câmera como distância focal, tamanho do pixel e distorções de sua lente;
• extrínsecos: orientação e posição da câmera com relação ao sistema de referência externo.

O modelo de câmera virtual é baseado na câmera de furo, experimento de Física para visualizar imagens em uma caixa com anteparo que gera uma imagem virtual do objeto observado. Esse modelo pode ser aproximado pela projeção cônica, onde se desloca o plano de projeção para um ponto entre o centro de projeção e o objeto, evitando que a imagem seja invertida. O parâmetro intrínseco é a distância focal.

Eixo óptico: Definido pela reta que passa pelo centro de projeção e fura a tela virtual no ponto denominado “centro óptico” ou “ponto principal”.

Para gerar as imagens em determinado instante, onde a câmera tem uma posição e o objeto visualizado outra, devemos executar transformações entre os sistemas de coordenadas do objeto, do mundo, da câmera e da tela. Para isso utiliza-se uma matriz de transformação $M_{obj}$, que utiliza as transformação básicas: rotação, escala, translação, etc. A matriz única que faz a transformação na API OpenGL é chamada de Modelview e é dada por :

$$ M_{view}=L_{at}\cdot M_{obj} $$

onde $L_{at}$ é matriz de transformação de câmera e $M_{obj}$ a matriz de modelagem do objeto.

Algumas transformações podem perder a informação de profundidade dos pontos o que acarreta na indeterminação de qual superfície deveria estar na frente de outra. Esse problema é resolvido levando-se o centro de projeção ao infinito e muda a transformação projetiva para paralela ortográfica.

Quando geramos um objeto, inicialmente definimos sua posição com relação à si mesmo, ou sistema de coordenadas local. Quando passamos para um sistema mais abrangente, chamado, mundo, utilizamos a matriz Model que é composta das transformações geométricas básicas (translação, rotação e escala). Como o objeto é feito de polígonos, podemos utilizar a face identificada após as transformações (que será visualizada pelo observador). O conjunto de faces é chamado de malha poligonal. Um formato comum de malha poligonal é o .obj, ou WaveFront. Exemplo:

    
# Blender3D v249 OBJ File
v 1.0000 -1.0000 -1.0000
v 1.0000 -1.0000 1.0000
v -1.0000 -1.0000 1.0000

f 5/1/1 1/2/1 4/3/1
    

onde v são vértices e f são faces (no formato: v/vt/vn), onde vn (vetor normal) e vt (coordenadas de textura). Cada face é representada por um polígono, um triângulo por exemplo. Se f 5/1/1, temos que 5 indica o quinto vértice da lista e os outros número a textura e a normal. Ao carregar o arquivo pode-se utilizar a função GL_TRIANGLES do OpenGL para processá-lo.

O sistema de coordenadas da visão implementa o ponto de vista de um observador ou câmera e translada essa entidade para a origem do sistema mundo. Sua matriz é chamada de View e é composta de Rotação e Translação. As coordenadas da câmera devem ser obtidas, assim como seu vetor normal e eixo, para transladá-la e rotacioná-la até a origem do sistema mundo. A matriz é como abaixo:

$$ R\cdot T=\begin{bmatrix} u_x & u_y & u_z & -u\cdot P_0 \\ v_x & v_y & v_z & -v\cdot P_0 \\ n_x & n_y & n_z & -n\cdot P_0 \\ 0 & 0 & 0 & 1 \end{bmatrix} $$

As malhas de polígonos são utilizadas para preencher e visualizar uma superfície. Normalmente são utilizados triângulos para tal processo, que depois recebem cores ou texturas para simular a aparência dos objetos. O processo de dividir o objeto em polígonos é chamado de tesselação, tecelagem ou mosaico. Quadrados e círculos podem ser desenhados com vários triângulos.

Um dos métodos utilizados para triangular um conjunto de pontos, ou vértices, é através da triangulação de Delaunay. Queremos ligar esses pontos com arestas, ou segmentos de reta, mas com certas restrições para que eles não se cruzem. Dado um conjunto de pontos S em um plano, uma subdivisão de S no plano que é determinada por um conjunto maximal de arestas (qualquer aresta que não está na triangulação vai intersectar alguma aresta pertencente à triangulação) que não se intersectam e seus vértices estão em S.

A triangulação é dependente do algoritmo utilizado. Exemplo: incremental. Em alguns casos, queremos maximizar alguma propriedade dos triângulos. Um caso comum é dos ângulos, já que trabalhar com triângulos muito pequenos (finos) pode não ser desejável.

O algoritmo Flip recebe um conjunto de pontos S no plano e aplica a triangulação até que todas as arestas ilegais foram removidas e daí obtemos a triangulação de Delaunay. Além deste há o algoritmo incremental. Ambos são $O(n^2)$ e fáceis de implementar.

As etapas envolvidas na renderização de um objeto são chamadas de pipeline. Ela pode ser para 2D ou 3D, utilizando-se das primitivas geométricas. Os seguintes são os passos básicos para geração da imagem:

1. Processamento dos vértices e suas instruções, em espaço de coordenadas normalizado;
2. Processamento de primitivas, suas transformações e posicionamento no espaço;
3. Geração e processamento dos fragmentos. Aplicação de cores e texturas;
4. Rasterização e geração da imagem.

Os pipelines podem ser fixos ou programáveis. O primeiro era o padrão até 2003, que dependia de algoritmos internos das placas de vídeo e era bem limitado no controle de alguns processos. O segundo é o padrão atual onde se utiliza shaders programáveis e uma linguagem própria de programação.

As APIs para computação gráfica mais comuns são OpenGL, DirectX, WebGL e Vulkan, onde cada uma tem seu próprio pipeline gráfico. Quando utilizamos o OpenGL precisamos definir uma janela para renderização da imagem. Alguns sistemas de janelas: FreeGLUT, GLFW, QT, SDL, etc. Nas janelas utilizamos um sistema cartesiano de coordenadas normalizadas, ou seja, $-1\leq x,y,z \leq 1$, com centro em $(0,0,0)$.

Quando simulamos a aplicação de uma luz em um objeto, parado ou em movimento, precisamos determinar como as sombras vão aparecer em determinadas superfícies e como modelar a projeção destes objetos em diferentes ângulos. Os efeitos da luz levados em conta são: reflexão, transmissão e absorção.

O Ray Tracing é utilizado para renderizar objetos em três direções, onde, partindo do ponto do observador, um vetor (raio) é projetado em cada um dos pixeis que fazem parte da cena.

O algoritmo de Gouraud é um técnica de interpolação utilizada para produzir sombreamento contínuo em superfícies que são representadas por malhas poligonais.

O algoritmo de linha de Bresenham visa aproximar uma linha reta entre dois pontos para desenho de imagens através de pixeis como uma matriz.

É o processo de mapear uma imagem na superfície de um objeto tridimensional. As texturas parecem mais “reais” porque lidam com propriedades da luz em cada polígono ou ponto configurado do objeto.

Uma textura é um objeto em 2D que é mapeado (envolve) o objeto 3D. Cada elemento de tamanho $s\times t$ é chamado de texel (texture element). As coordenadas de texturas estão definidas no intervalo $[0,1]$.

O mapeamento envolve identificar o ponto visualizado com a posição na textura para exibição correta da parte do objeto. Tipos de mapeamento, com coordenadas $uv$:

• Planar: mapeamento de forma ortogonal. O efeito é ruim quando há vetores normais perpendiculares;
• Cúbico: mapeamento para seis faces de um cubo;
• Esférico: mapeamento através de coordenadas polares esféricas;
• Cilíndrico: mapeamento utilizando polares cilíndricas.

Como pixeis não são texeis, as vezes o polígono é maior / menor do que a textura. Para isso deve-se aplicar filtros. Há dois tipos básicos:

• Nearest: escolhe o texel mais próximo por coordenada;
• Linear: escolhe o texel por aplicação de interpolação dos vizinhos e usa um valor aproximado.

O problema do serrilhado ocorre quando renderizamos uma imagem utilizando pixeis e há subamostragem na conversão dos dados, que é um problema de perda de informação da imagem. Isso pode ser evitado utilizando uma amostragem duas vezes maior que a frequência máxima do objeto. Isso pode resultar em bordas irregulares ou na aparência de padrões de alta frequência na imagem, conhecidos como padrões moiré.

Antialiasing é o processo de reduzir ou eliminar essas distorções suavizando as bordas irregulares ou padrões de alta frequência. Isso pode ser feito superamostrando a imagem ou usando técnicas como filtragem ou mesclagem. O oversampling envolve o aumento da resolução da imagem digital, o que pode reduzir a aparência de bordas irregulares, mas também pode aumentar os requisitos computacionais para renderizar a imagem.

A filtragem envolve o uso de um algoritmo matemático para suavizar as bordas irregulares ou padrões de alta frequência na imagem. Isso pode ser feito usando uma variedade de técnicas, incluindo filtragem Gaussiana, filtragem de caixa ou filtragem bilinear. Cada uma dessas técnicas tem seus próprios pontos fortes e fracos, e a escolha da técnica dependerá da aplicação e dos requisitos específicos.

A mesclagem envolve a mesclagem de pixels adjacentes, o que pode reduzir a aparência de bordas irregulares ao criar uma transição mais suave entre os pixels adjacentes. Isso pode ser feito usando uma variedade de técnicas, incluindo supersampling, multisampling ou amostragem adaptativa.

A visualização de um objeto depende da iluminação do ambiente onde ele se encontra, analisando as propriedades básicas da luz e reflexão de outros elementos. Para isso são utilizados modelos de iluminação para aproximação o comportamento físico da luz e seus efeitos nos objetos próximos.

A luz ambiente provê um nível geral de brilho para uma cena e cada superfície irá refletir parte da luz conforme suas propriedades. O nível de luz tem um parâmetro chamado intensidade $I_a$ que varia no intervalo $[0,1]$.

Os dois tipos de reflexão principais são:

Difusa: Quantidade da luz incidente varia com a orientação da superfície levando em conta a direção da luz.

Especular: Dado um ângulo de reflexão especular, representa a reflexão da luz incidente na área ao redor do ângulo.

Modelo de Phong: define a intensidade da reflexão especular, que é proporcional ao $cos^{n_s}\phi$ onde $0º\leq \phi\leq 90º$ e $n_s$ é o expoente de reflexão especular.

Deve-se combinar a reflexão especular e difusão para modelar a luz nos objetos.

Referências:

1. Computação Gráfica - Alaor Cervati Neto - ICMC USP
2. Computação Gráfica I - Anselmo Montenegro - UFF
3. Principais algoritmos de visibilidade - Unicamp
4. Computer Graphics Tutorial

< 19 - Compiladores > 21 - Engenharia de Software