O princípio fundamental da contagem afirma que quando um evento qualquer é composto por $n$ etapas sucessivas e independentes e temos $m_i$ elementos para distribuir em cada etapa, o total de possibilidades é dado por

$$ m_1\cdot m_2\cdot...\cdot m_n=\prod_i^n m_i $$

Exemplo: Para distribuir 3 medalhas, ouro, prata e bronze, entre 4 competidores, temos:

Ouro: 4 possibilidades
Prata: 4-1=3 possibilidades
Bronze: 4-2=3-1=2 possibilidades

Isso acontece porque quem ganhou ouro está fora da lista da de prata, quem ganhou ouro ou prata está fora da lista de bronze e assim por diante. Então

$$ D=4\cdot3\cdot2=24\; \text{possibilidades} $$

No caso de $m_i$ ser uma sequência natural decrescente, temos um fatorial:

$$ m!=m(m-1)(m-2)...1 $$

Se temos um conjunto com n elementos e desejamos formar grupos com $p$ itens ($p\leq n$) , todos distintos, sem se importar com a ordem, utilizamos o chamado "arranjo simples" para contar as possibilidades:

$$ A_{n,p}=\frac{n!}{(n-p)!} $$

Uma permutação simples ocorre quando temos $n$ elementos e fazemos um arranjo de $n$, ou seja

$$ P_n=A_{n,n}=\frac{n!}{(n-n)!}=\frac{n!}{1}=n! $$

onde a contagem resulta no fatorial.

A permutação com repetição é dada por:

$$ P_n^{k,j}=\frac{n!}{k!\cdot j!} $$

Se temos um conjunto com $n$ elementos e os tomamos de $p$ em $p$, a combinação é qualquer subconjunto de $A$ formado pelos $p$ elementos onde descontamos agrupamentos com permutação dos mesmos elementos:

$$ C_{n,p}=\frac{n!}{p!(n-p)!} $$

Funções geradoras, por exemplo, polinomiais, conectam coeficientes inteiros de um polinômio com a resposta de um problema de contagem em combinatória. Um polinômio é da forma

$$ p(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0 $$

Outro exemplo é uma série de potências, uma soma infinita por exemplo, que também pode ser uma função geradora.

$$ |x| < 1,\;1+x+x^2+...+x^n+...=\frac{1}{1-x} $$

Exemplo: Quantas são as soluções inteiras da equação abaixo, sabendo que $x_1$ e $x_2$ pertencem ao conjunto {1,2,3} e $x_3$ pertence ao conjunto {2,3,5}?

$$ x_1+x_2+x_3=6 $$

Cada variável $x_1$ deve ser associada a um polinômio $p_i$ de tal forma que os expoentes vão representar as distintas possibilidades de valores que cada variável pode assumir:

$$ p_1(x)=x^1+x^2+x^3\\ p_2(x)=x^1+x^2+x^3\\ p_3(x)=x^2+x^3+x^5 $$

A solução é dada pela função geradora, que é o produto dos três polinômios:

$$ F(x)=p_1(x)\cdot p_2(x)\cdot p_3(x) $$

De forma que vamos obter um novo polinômio e a solução é dada pelo coeficiente que acompanha a variável de potência 6:

$$ F(x)=x^4+3x^5+5x^6+6x^7+5x^8+4x^9+2x^{10}+x^{11} $$

Sejam $\mathcal{A},\mathcal{B}$ dois conjuntos não vazios com elementos em comum. Queremos avaliar a seguinte equação:

$n(\mathcal{A}\;\cup\;\mathcal{B})=n(\mathcal{A})+n(\mathcal{B})$

A união de itens de um com o de outros, sem excluir os iguais, vai nos levar a um valor incorreto, ou seja, precisamos excluir os elementos existentes nos dois:

$n(\mathcal{A}\;\cup\;\mathcal{B})=n(\mathcal{A})+n(\mathcal{B})-n(\mathcal{A}\;\cap\;\mathcal{B})$

Mas o que acontece quando temos 3 conjuntos?

$n(\mathcal{A}+\mathcal{B}+\mathcal{C})=?$

Bem, precisamos remover as intersecções entre cada um deles:

$n(\mathcal{A}+\mathcal{B}+\mathcal{C})=n(\mathcal{A})+n(\mathcal{B})+n(\mathcal{C})-n(A\;\cap\;\mathcal{B})-n(\mathcal{A}\;\cap\;\mathcal{C})-n(\mathcal{B}\;\cap\;\mathcal{C})$

Porém, esse valor ainda está incorreto porque estamos “descontando” duas vezes alguns elementos. Precisamos adicionar os itens da intersecção tripla:

$n(\mathcal{A}+\mathcal{B}+\mathcal{C})=n(\mathcal{A})+n(\mathcal{B})+n(\mathcal{C})-n(A\;\cap\;\mathcal{B})-n(\mathcal{A}\;\cap\;\mathcal{C})-n(\mathcal{B}\;\cap\;\mathcal{C})+n(\mathcal{A}\;\cap\;\mathcal{B}\;\cap\;\mathcal{C})$

O problema de enumerar partições é o mesmo do que contar os subconjuntos diferentes de uma determinada contagem. Devemos escolher n elementos em m conjuntos e achar as possíveis combinações. Por exemplo: De quantas maneiras podemos repartir 6 pessoas em 3 grupos distintos ficando 2 pessoas em cada grupo?

Como a ordem não importa (AB=BA), podemos usar combinação:

$\frac{C_6^2}{G_1}\cdot \frac{C_4^2}{G_2}\cdot \frac{C_2^2}{G_3}=90$

Esse problema também pode ser resolvido com a fórmula de permutação com repetição.

Caso o problema exija a exclusão de casos múltiplos, o problema da contagem fica na forma:

$$ \frac{C_n^k \cdot C_{n-k}^k...}{k!} $$

Para enumerarmos grafos, árvores e redes podemos utilizar o método gráfico para listar todas as possibilidades então ou contá-las ou utilizar o princípio multiplicativo para obter o resultado.

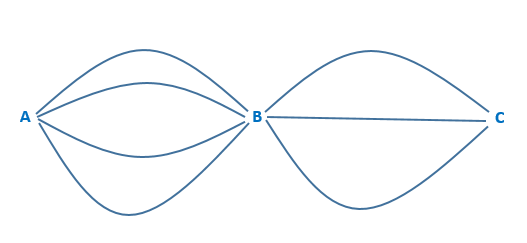
Exemplo de grafo.

Na imagem acima podemos considerar que cada letra representa uma cidade (A, B e C) e as linhas que as conectam são os elos. De quantas maneiras distintas podemos ir de A até C?

Pelo princípio multiplicativo, temos 4 caminhos de A para B e 3 caminhos de B para C, logo

$P=P_1\cdot P_2=4\cdot 3=12$

Para ver exemplo de código desta seção, veja [4].

Podemos enumerar subsequências de um determinado conjunto recursivamente. Por exemplo, vamos enumerar todas as subsequências não vazias de I={1,2,3,4}

1
1 2
1 2 3
1 2 3 4
1 2 4
1 3
1 3 4
1 4
2
2 3
2 3 4
2 4
3
3 4
4

A ordem utilizada é chamada de lexicográfica. Quando fazemos um código recursivo podemos olhar para subsequências de tamanhos distintos a cada iteração para resolver mais rapidamente o problema, excluindo obviamente os casos repetidos na medida que avançamos no vetor de entrada (ver [4]).

Esse tipo de permutação é um rearranjo dos elementos de um conjunto apenas em determinadas posições. Exemplo: Quantas placas de carros podemos formar com 3 letras e 4 números em sequência?

$\underline{26} \; \underline{26} \; \underline{26}\; \underline{10}\;\underline{10}\;\underline{10}=17576000$

Porém, nesse caso, todos os elementos podem ser repetidos em todas as casas. Caso tivéssemos um problema onde não podemos repetir o elemento anterior na próxima casa, teremos uma permutação simples:

$\underline{26} \; \underline{25} \; \underline{24}\; \underline{10}\;\underline{9}\;\underline{8}=11232000$

Referências:

1. Funções geradoras e problemas de contagem - IME UFRGS
2. Princípio da inclusão-exclusão
3. Resumo de análise combinatória
4. Algoritmos de enumeração

< 1 - Álgebra Linear > 3 - Cálculo Diferencial e Integral