O que é: Conjunto de equações lineares (onde a potência maior é 1) com incógnitas que devem ser descobertas para sua solução. Para que seja possível resolver um sistema de $n$ incógnitas ($ n \geq 2 $) precisamos de pelo menos n equações.

Há duas formas práticas de solução quando o número de equações é pequeno ($n\leq3$):

Substituição: Isolamos uma das variáveis em alguma equação e a substituímos em outra equação. Por exemplo:

$$ y=2-x \\ 4x+y=2\\ ---------\\ 4x+(2-x)=2\\ 3x+2=2\\ x=0 \Rightarrow y=2 $$

Eliminação: Somamos duas equações para eliminar uma das variáveis e descobrir o valor de outra. Por Exemplo:

$$ 3x-y=7 \quad [1]\\ 2x+y=8 \quad [2]\\ = 5x+0y=7+8 \Rightarrow x=3\\ \Rightarrow 3(3)-y=7 \Rightarrow 9-y=7 \Rightarrow y=2 $$

Para $n\geq 2$, podemos utilizar o método de eliminação de Gauss, que consiste em um algoritmo para transformar a matriz original em uma matriz triangular para resolver o sistema mais facilmente. Ver exemplo em: Eliminação de Gauss - Wikipédia

Definição: Um espaço vetorial é um conjunto munido de uma operação de adição e de uma operação de multiplicação por escalar que respeita as seguintes propriedades:

Dado $E$, qualquer um dos seguintes conjuntos: $V^3$, conjunto dos vetores da Geometria do espaço, $R^n$, conjunto das n-tuplas ordenadas de números reais, ou $F(I)$, conjunto das funções definidas no intervalo $I\subset R$ e com valores em $R$, temos

1. $\forall\;u,v,w \in E \quad (u+v)+w=u+(v+w)$
2. $\forall\;u,v\in E \quad u+v=v+u$
3. $\exists\;0\in E\;|\;\forall u\in E\quad u+0=0+u$
4. $\forall\;u\in E,\exists\;(-u)\in E\;|\;u+(-u)=(-u)+u=0$
5. $\forall\;\alpha,\beta\in R,\;\forall\;u,v\in E \; \alpha(u+v)=\alpha u+\alpha v$
6. $\forall\;\alpha,\beta \in R,\; \forall\;u \in E \quad (\alpha +\beta)u=\alpha u+\beta u$
7. $\forall\;\alpha,\beta \in R,\;\forall\;u\in E \quad \alpha(\beta u)=(\alpha \beta)u$
8. $\forall\;u \in E \quad 1u=u$

Um subconjunto $S$ de um espaço vetorial $V$ é chamado subespaço vetorial de $V$ se:

1. O vetor nulo de $V$ pertence a $S$;
2. Se os vetores $u$ e $v$ de $V$ estão em $S$, então $u+v$ também pertence a $S$;
3. Se o vetor $u$ de $V$ está em $S$ e $\lambda\in R$ é um escalar qualquer, então $\lambda u$ também pertence a $S$.

Seja $\mathcal{B}$ é um conjunto de vetores. Ele será uma base para um espaço vetorial $V$ se:

1. gera $V$ e;
2. é linearmente independente.

Exemplo: No $\mathbb{R^n}$ temos que

$$\vec{e}_1=[1 \; 0\;0 ... \; 0], \vec{e}_2=[0 \; 1\;0 ... \; 0],...,\vec{e}_n=[0 \; 0\;0 ... \; 1]$$

é um conjunto linearmente independente e que gera o espaço vetorial $\mathbb{R}^n$.

A soma de dois subespaços de $V$, $W_1, W_2$ , é dada por

$W_1+W_2=\{u\in V|u=v_1+v_2, v_1\in W_1\;e\;v_2\in W_2\}$

Sejam $W_1, W_2$ subespaços do espaço vetorial $V$. Quando $W_1\cap\ W_2=\{\bar{0}\}$ , chamamos a soma $W_1+W_2$ de soma direta e usamos a notação $W_1\oplus W_2$.

Exemplo: Sejam os subespaços: $W_1=\{(x,y,z) \in \mathbb{R}^3 | (x,y,z)=(2t,-t,t),t \in \mathbb{R} \}$ $W_2=\{(x,y,z)\in\mathbb{R}^3|(x,y,z)=(m,m,3m),m\in\mathbb{R}\}$

Determine se $W_1+W_2$ é uma soma direta.

Solução: Precisamos avaliar se a intersecção dos subespaços resulta no vetor nulo. Estamos procurando então por:$(2t,-t,t)=(m,m,3m)$ Para isso, montamos um sistema:

$$ 2t=m \\ -t=m \\ t=3m $$

De forma que, $t=0, m=0$. Logo, o único ponto em comum é $\bar{0}$. Logo, a soma é direta.

O objetivo da programação linear é a obtenção da melhor solução (solução ótima) para problemas cujos modelos associados são lineares. Exemplo: Se temos duas variáveis, $x$ e $y$, e as equações dadas são do tipo:

$a_1\cdot x+a_2\cdot y=b$

então podemos usar as ferramentas de programação linear para encontrar que valores de x e y devemos utilizar para encontrar b.

Passos:

1. Identificar as variáveis desconhecidas a serem determinadas - variáveis de decisão;
2. Listar as restrições do problema em função das variáveis de decisão;
3. Identificar o objetivo ou critério de otimização do problema - função linear com as variáveis de decisão.

Exemplo: Suponha que uma fábrica de móveis fabrique dois tipos de objetos: cadeiras e mesas. Uma cadeira precisa de 5 tábuas e 10 horas de trabalho enquanto uma mesa necessita de 10 tábuas e 15 horas de trabalho. Levando em conta que a fábrica possui 400 tábuas e 450 horas de trabalho disponíveis e que o lucro por cadeira é de $\text{R\$180,00}$ e o por mesa é de $\text{R\$320}$, otimize as variáveis para obter o maior lucro possível.

Primeiro vamos escrever as equações para cada recurso. Nomeando a quantidade de cadeiras por $x_1$ e a quantidade de mesas por $x_2$ , temos

I) $5x_1+20x_2\leq400$ ( tábuas )

II) $10x_1+15x_2\leq450$ ( horas )

III) $L=180x_1+320x_2$ ( lucro )

Primeiros podemos usar o método gráfico tentar resolver o problema. Vamos descobrir o valor de $x_1$ se $x_2=0$. Pela equação (I), temos

$5x_1=400\Rightarrow x_1=400/5=80$

No caso de $x_1=0$, temos, também equação (I),

$20x_2=400 \Rightarrow x_2=400/20=20$

Os pontos $x_1=80$ e $x_2=20$ podem ser colocados em um gráfico bidimensional.

Fazendo o mesmo que fizemos para equação I) na equação II) encontramos: $x_2=30$ e $x_1=45$.

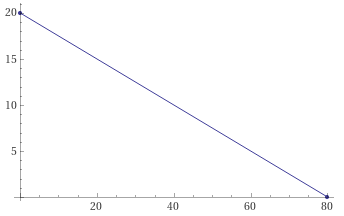
Os dois gráficos pode ser sobrepostos para obtermos a área viável para o problema.

A solução do problema está nos vértices dentro da área viável:

$$ P_1=(0,20) \\ P2=?\\ P3=(45,0)$$

Como encontramos o ponto $P2$? Podemos resolver o seguinte sistema (inequações I) e II) transformadas em equações)

$$ 5x_1+20x_2=400\\ 10x_1+15x_2=450 $$

onde obtemos $P_2=(24,14)$.

Utilizando esses pontos na equação III), encontramos que o valor máximo de lucro:

$$ L_1=180\cdot0+320\cdot20=6400\\ L_2=180\cdot24+320\cdot14=8800\\ L_3=180\cdot45+320\cdot0=8100 $$

A solução ótima é então: 24 cadeiras e 14 mesas.

Podemos resolver o mesmo problema usando o método analítico. Considerando o sistema resolvido anteriormente, de resultado (24,14), precisamos verificar se essa solução satisfaz:

IV) $x_1\geq0$

V) $x_2\geq 0$

Já sabemos que esse par obtido é viável e é a resposta, porém, em qualquer problema, precisamos avaliar as outras combinações, $x_1=0$ e $x_2>0$ e $x_1>0$ e $x_2=0$. Resolvendo as equações para I) e II) em cada combinação, podemos checar se as inequações continuam verdadeiras. Por exemplo:

$$ 5x_1+20x_2=400\\ x_2=0\\ x_1=80 $$

Logo,

$$ 10\cdot80+0\leq 450 \; \text{verdadeiro} $$

E assim vamos elencando as soluções e testando os resultados. Com cada ponto podemos verificar o lucro e chegar na mesma solução da obtida pelo método gráfico.

Seja $T$ uma função que leva vetores de um espaço $V$ para outro W, $T:V\rightarrow W$. Chamamos essa função de transformação linear se:

1. $T(\alpha v)=\alpha T(v), v\in V \;e\; \alpha \in \mathbb{R}$
2. $T(u+v)=T(u)+T(v), \;com \;u,v\in V$

A imagem de $T$ é o conjunto $Im(T)$ dado por

$Im(T)=\{ w \in W | T(v) = w, \text{ para algum } v \in V \}$

onde $Im(T)$ é um subespaço vetorial de $W$.

O núcleo de $T$ é o conjunto $ker(T)$ dado por $ker(T)=\{v\in V|T(v)=\bar{0} \}$ onde $ket(T)$ é um subespaço vetorial de $V$. Teorema do núcleo e da imagem: Sejam $V$ e $W$ espaços vetoriais de dimensão finita e $T:V\rightarrow W$ uma transformação linear. Temos que

$dim(V)=dim(ker(T))+dim(Im(T))$

Seja $T:V\rightarrow V$ uma transformação linear. Dizemos que o escalar $\lambda$ é um autovalor de $T$ se existir um vetor não nulo $v\in V$ tal que

$$ T(v)=\lambda v $$

Dizemos que esse vetor $v$ é o autovetor de $T$ associado ao autovalor $\lambda$.

Polinômio característico: Seja $A$ a matriz associada ao operador linear $T: V\rightarrow V$ em relação a uma base $B$, os autovalores de $T$ são as soluções da equação:

$$ det(A-\lambda I)=0 $$

O polinômio característico é dado por $p(\lambda)=det(A-\lambda I)$.

Polinômio minimal: Seja $A$ uma matriz quadrada sobre $\mathbb{R}$ e $J(A)$ , não vazio, o conjunto de todos os polinômios $f(t)$ tais que $f(A)=0$. Se $m(t)$ é o polinômio mônico de menor grau em $J(A)$, então, se há um polinômio mínimo em $A$, ele é único. Para encontrar $m(t)$ seguimos os seguintes passos:

1. Achar o polinômio característico $p(\lambda)$;
2. Calcular as raízes de $p(\lambda)$;
3. Encontrar polinômios $m_i(t)$ que dividem $p(\lambda);$
4. Calcular $m_i(A)$ e encontrar aquele em que $m_j(A)=0.$

Seja $T:V\rightarrow V$ um operador linear com $B=\{v_1,v_2,...,v_n \}$ uma base de $V$. Se cada $v_i$ for um autovetor de $T$ associado a um autovalor $\lambda_i$, então

$$ P^{-1}AP=D $$

onde $P$ é a matriz formada com a coluna $i$ igual a $v_i$, $A$ é a matriz de $T$ na base $B$ e $D$ é a matriz diagonal com $[D]_{ii}=\lambda_i$.

Seja $V$ um espaço vetorial sobre o corpo dos reais. Chamamos de produto interno uma função que associa cada par de vetor $u,v$ em $V$ com um número real denotado por $\langle u,v \rangle $, tal que

1. $\langle u,v\rangle;\geq 0,$ para todo $u\in V$
2. $\langle u,u\rangle=0,$se e somente se $u=\bar{0}$
3. $\langle u_1+u_2,v\rangle=\langle u_1,v\rangle+\langle u_2,v\rangle$
4. $\langle\alpha u,v\rangle=\alpha\langle u,v \rangle$
5. $\langle u,v\rangle=\langle v,u\rangle$

Seja $\mathcal{B}$ uma base ortogonal de $\mathbb{R}^n$. Então, qualquer vetor $\vec{v}\in \mathbb{R}^n$ pode ser representado como

$$ \vec{v}=\frac{\vec{v}\cdot\vec{v_1}}{\vec{v_1}\vec{v_1}}\cdot \vec{v_1}+\frac{\vec{v}\cdot\vec{v_2}}{\vec{v_2}\vec{v_2}}\cdot \vec{v_2}+...+\frac{\vec{v}\cdot\vec{v_n}}{\vec{v_n}\vec{v_n}}\cdot \vec{v_n} $$

ou, de outra maneira, como projeção

$$ \vec{v}=proj_{\vec{v_1}}\vec{v}+proj_{\vec{v_2}}\vec{v}+...+proj_{\vec{v_n}}\vec{v} $$

onde $proj_{\vec{v_i}}=c_i=\frac{\vec{v}\cdot\vec{v_i}}{\vec{v_i}\cdot\vec{v_i}}$ e temos os coeficientes para gerar o vetor $\vec{v}$.

Para que vetores ortogonais sejam ortonormais, basta que os normalizemos:

$$ \vec{u}_n=\frac{\vec{u}}{||\vec{u}||} $$

Então, uma base ortonormal é o conjunto de vetores ${\vec{v_1},\vec{v_2},...,\vec{v_n}}$ se para qualquer índice i $||\vec{v_i}||=1$ e com $i\ne j$ temos que $\vec{v_i}\cdot\vec{v_j}=0$.

A projeção ortogonal de um vetor $\vec{y}$ na direção de $\vec{w}$ é dada por

$$ \vec{k}=proj_{\vec{w}}\vec{y}=\frac{\vec{y}\cdot\vec{w}}{\vec{w}\cdot\vec{w}}\vec{w} $$

A projeção ortogonal de um vetor $\vec{y}$ em um subespaço de F gerado por $\vec{w_1},\vec{w_2}$ é dada pela equação:

$$ \vec{k}=proj_F\vec{y}=proj_{\vec{w_1}}\vec{y}+proj_{\vec{w_2}}\vec{y}= \frac{\vec{y}\cdot\vec{w_1}}{\vec{w_1}\cdot\vec{w_1}}\vec{w_1}+\frac{\vec{y}\cdot\vec{w_2}}{\vec{w_2}\cdot\vec{w_2}}\vec{w_2} $$

Quando o vetor $\vec{k}$ não é combinação linear do subconjunto ortogonal de F, podemos calcular a projeção por $\vec{y}-\vec{k}$, onde o resultado é ortogonal à F.

No plano, há três tipos de movimentos rígidos: translações, reflexões e rotações (em torno de um ponto). No espaço, a reflexão é relativa a um plano e a rotação é dada em torno de um eixo orientado. O teorema de Euler diz que todo movimento rígido, no plano ou no espaço, pode ser obtido por uma sequência de translação, rotação e reflexão (ou omitindo uma delas).

O método de mínimos quadrados é útil para resolver sistemas de equações onde há inconsistências entre as relações de variáveis, ou seja, são sistemas impossíveis. Neste caso, procuramos uma aproximação da solução através de uma projeção do vetor de coeficientes $\vec{b}$ da seguinte relação

$$ A\vec{x}=\vec{b} $$

Prosseguimos no problema encontrando a transposta da matriz $A$, que usaremos para achar um novo sistema que será resolvido.

$$ A^T\vec{b}=\vec{y} $$

Fazemos

$$ A^TA\vec{x}=\vec{y} $$

resolvemos esse novo sistema e teremos a aproximação desejada.

Seja $V$ um espaço vetorial. Definimos um funcional linear como

$$ \Phi:V\rightarrow \mathbb{R} $$

onde

1. $\Phi(v+w)=\Phi(v)+\Phi(w), \forall v,w\in V$
2. $\Phi(\lambda v)=\lambda\Phi(v), \forall v\in V$

O conjunto de todos os funcionais lineares é chamado de espaço dual:

$$ V^*=\{\Phi:V\rightarrow \mathbb{R}\;|\;\Phi\; \text{é funcional \; linear\}} $$

O espaço dual também é um espaço vetorial.

O teorema de representação para funções lineares nos diz que dado um $\Phi\in V^*$ temos que existe um único $v\in V$ tal que

$$ \Phi(w)=\langle v,w \rangle \;, \forall \; w\in V $$

Seja V um espaço vetorial. O operador adjunto, $T^*:V\rightarrow V$, de um operador linear em V, é definido por

$$ \langle T(u),v \rangle=\langle T(u,T^*(v) \rangle \;, \forall \;u,v\in V $$

Todo operador linear possui um e apenas um operador adjunto.

Dado um espaço vetorial $V$ e uma transformação linear $T$, temos:

Operador Simétrico: $\langle T(u),v\rangle=\langle u,T(v)\rangle$ (muda a aplicação de T do primeiro para segundo vetor);

Operador Unitário: $T^*=T^{-1}$ (preserva o produto interno e norma);

Operador Normal: $T^*T=TT^*$ (todo operador auto-adjunto ou unitário é normal);

Seja $A\in M_{n\times n}(\mathbb{R})$ simétrica. Então $A$ é diagonalizável sobre os reais. Existe uma matriz ortogonal $P$ tal que

$$ A=P\cdot D\cdot P^{-1}, \; P^{-1}=P^T $$

No $\mathbb{R}^n$ se $\mathcal{A}$ e $\mathcal{B}$ são bases, temos que $M_{\beta}^\alpha$ , a matriz mudança de base, é ortogonal se e somente se $\mathcal{B}$ é ortonormal. Então, de outra forma, existe uma base ortonormal $\mathcal{B}$ de autovetores de $A$, tal que

$$ Av_i=\lambda_i v_i, \; \lambda=1,...,n $$

A forma canônica de Jordan possibilita a representação de uma matriz ou operador linear por outra matriz, que não é diagonal, mas é triangular inferior no corpo dos reais.

Referências:

1. Álgebra Linear - UFRGS
2. Álgebra Linear - Wikipédia
3. Álgebra Linear - Matemática Universitária - Prof. Renan
4. Programação Linear - André Brochi - YouTube
5. Polinômio Minimal - IFSul

> 2 - Análise Combinatória