Vamos usar o teorema de Laplace para encontrar o $det(A)$, onde $A$ é a matriz $5\times 5$ dada. Como a última coluna é composta de quatro zeros e a segunda linha de dois zeros, vamos utilizar o elemento $A_{2,5}$. Precisamos calcular:

$$ det(A)=\sum_{i=1}^5 a_{2i}C_{2i}=a_{21}C_{21}+a_{22}C_{22}+...+a_{25}C_{25} $$

Onde $C_{ij}$ é o cofator, calculado como:

$$ C_{ij}=(-1)^{i+j}\cdot D'_{ij} $$

e $D'_{ij}$ o determinante da matriz resultante quando eliminamos a linha $i$ e coluna $j$. Logo

$$ a_{21} = 4, C_{21}=(-1)^{2+1}\cdot \begin{pmatrix} 2 & 3 & 4 & 5 \\ 6 & 7 & 2 & 0 \\ 9 & 10 & 3 & 0 \\ 12 & 13 & 4 & 0 \end{pmatrix}=0 \\ a_{22} = 3, C_{22}=(-1)^{2+2}\cdot \begin{pmatrix} 1 & 3 & 4 & 5 \\ 8 & 7 & 2 & 0 \\ 12 & 10 & 3 & 0 \\ 16 & 13 & 4 & 0 \end{pmatrix}=0 \\ a_{23} = 4, C_{23}=(-1)^{2+3}\cdot \begin{pmatrix} 1 & 2 & 4 & 5 \\ 8 & 6 & 2 & 0 \\ 12 & 9 & 3 & 0 \\ 16 & 12 & 4 & 0 \end{pmatrix}=0 \\ a_{24} = 4, C_{24}=(-1)^{2+4}\cdot \begin{pmatrix} 1 & 2 & 3 & 5 \\ 8 & 6 & 7 & 0 \\ 12 & 9 & 10 & 0 \\ 16 & 12 & 13 & 0 \end{pmatrix}=0 \\ a_{25} = 4, C_{25}=(-1)^{2+5}\cdot \begin{pmatrix} 1 & 2 & 3 & 4 \\ 8 & 6 & 7 & 2 \\ 12 & 9 & 10 & 3 \\ 16 & 12 & 13 & 4 \end{pmatrix}=0 \\ det(A)=0 $$

Resposta : e

Vamos identificar os vetores diretores de cada reta:

$$ \vec{r}=(4,-2,3) \\ \vec{s}=(1,-1,2) $$

Vamos calcular primeiro o produto escalar

$$ \vec{r}\cdot \vec{s} = 4\cdot (-1) + (-2)\cdot (-1) + 3\cdot 2=4+2+6=12 $$

Isso implica que as retas não são perpendiculares. Podemos checar se são não-coincidentes:

$$ \vec{r}=k\vec{s} \Rightarrow \\ (4,-2,3)=(k, -k, 2k) \Rightarrow \\ \nexists \; k $$

Agora podemos calcular o ângulo entre os vetores:

$$ cos(\beta)=\frac{\vec{r}\cdot \vec{s}}{||\vec{r}|| ||\vec{s}||} \\ ||\vec{r}||=\sqrt{16+4+9}=29^{1/2} \\ ||\vec{s}||=\sqrt{1+1+4}=6^{1/2} \\ cos(\beta)=\frac{12}{\sqrt{174}}\sim 0,91 $$

O que implica que não são ortogonais. Vamos analisar se são coplanares calculando o determinante da matriz de coeficientes dos vetores:

$$ det(A)= \begin{pmatrix} 4 & -2 & 3 \\ 1 & -1 & 2 \\ \end{pmatrix}=4(-4+3)-(-2)(8-3)+3(-4+2)=\\ -4+10-6=0 $$

Ou seja, as retas estão no mesmo plano.

Resposta: b

A excentricidade é um parâmetro associado a todas as figuras geradas pela intersecção entre um plano e um cone (secções cônicas). A circunferência é um caso particular de uma elipse. A elipse tem excentricidade entre 0 e 1 enquanto a circunferência tem excentricidade igual a 0.

Resposta: a

Precisamos analisar a inequação abaixo:

$$ \frac{|x-2|}{x^2}>1 $$

Começamos notando que $x-2=x^2$ ou $x-2=-x^2$. A primeira equação não tem solução nos reais. A segunda pode ser escrita como:

$$ (x-1)(x+2)=0 \Rightarrow x=1, \; x=-2 $$

Então $-2 < x < 1$.

Resposta: e (Questão anulada)

Vamos calcular o limite:

$$ \lim_{n\rightarrow \infty} (\frac{n^2+1}{n^7-2})^{1/n} = \\ = \lim_{n\rightarrow \infty} (n^2+1)^{1/n} \lim_{n\rightarrow \infty} (\frac{1}{n^7-2})^{1/n} \\ $$

Vamos olhar cada um separadamente:

$$ \lim_{n\rightarrow \infty} (n^2+1)^{1/n}=\lim_{n\rightarrow \infty} (n^2)^{1/n} \\=\lim_{n\rightarrow \infty} n^{2/n} = 1 \\ \lim_{n\rightarrow \infty} (\frac{1}{n^7-2})^{1/n} = \lim_{n\rightarrow \infty} n^{-7/n} = 1 $$

Logo, o limite é 1.

Resposta : a

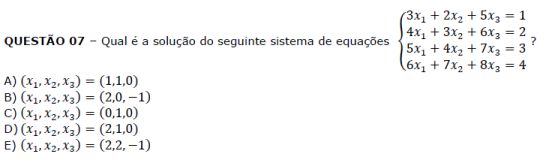
Vamos usar o método de Gauss para resolver o sistema. Primeiro o escrevemos como uma matriz $4\times 4$.

$$ \begin{pmatrix} 3 & 2 & 5 & 1 \\ 4 & 3 & 6 & 2 \\ 5 & 4 & 7 & 3 \\ 6 & 7 & 8 & 4 \end{pmatrix} \rightarrow L_4=L_4-2L_1 \\ \begin{pmatrix} 3 & 2 & 5 & 1 \\ 4 & 3 & 6 & 2 \\ 5 & 4 & 7 & 3 \\ 0 & 3 & -2 & 2 \end{pmatrix} \rightarrow L_3=L_3-(5/4)L_1 \\ \begin{pmatrix} 3 & 2 & 5 & 1 \\ 4 & 3 & 6 & 2 \\ 0 & 4 & -1 & 1 \\ 0 & 3 & -2 & 2 \end{pmatrix} \rightarrow L_4=L_4-(4/3)L_3 \\ \begin{pmatrix} 3 & 2 & 5 & 1 \\ 4 & 3 & 6 & 2 \\ 0 & 4 & -1 & 1 \\ 0 & 0 & -1 & 1 \end{pmatrix} \\ $$

Disso tiramos que $z=-1$. Substituindo para a terceira equação, temos que $y=0$ e então $x=2$.

Resposta : b

Pode usar a fórmula com a inclinação das curvas para calcular o valor de $m$.

$$ tan(\beta)=|\frac{m_1-m_2}{1+m_1\cdot m_2}| \\ tan(45º)=1=|\frac{-3+2/m}{1+(-3\cdot -2/m)}| \\ 1=|\frac{-3m+2}{m+6}| \\ \text{caso 1:} \\ 1= \frac{-3m+2}{m+6} \\ m=-1 \\ \text{caso 2:} \\ -1=\frac{-3m+2}{m+6} \\ m=4 $$

Resposta: d

O complemento da função $f$ é dado por:

$$ \bar{f}=\overline{(x+\bar{y})(yz+x\bar{y})} $$

Onde podemos resolver cada parte separadamente:

1. $\overline{(x+\bar{y})(yz+x\bar{y})}=\overline{x+\bar{y}}+\overline{(yz)+(x\bar{y})}$
1. $\overline{x+\bar{y}}=\bar{x}y$
2. $\overline{(yz)+x\bar{y}}=\overline{yz}\overline{x\bar{y}}=(\bar{y}+\bar{z})(\bar{x}+y)$
2. $((\bar{y}\bar{x})+(y\bar{x}))+(x\bar{z})=\bar{x}+(y\bar{z})$

Logo, obtemos que a resposta é:

$$ \bar{f}=\bar{x}+y\bar{z} $$

Resposta : a

Vamos dividir o sistema em duas funções:

$$ f_1(x,y)=xe^u+yu=1 \\ f_2(x,y)=2x^2v+y^2e^u=1 $$

Precisamos diferenciar cada função para $x$ e para $y$, não esquecendo de usar a regra da cadeia.

$$ \frac{\partial f_1}{\partial x}=0=e^u x\frac{\partial u}{\partial x}+y\frac{\partial u}{\partial x} \Rightarrow \frac{\partial u}{\partial x}=\frac{-e^u}{xe^u+y} \\ \frac{\partial f_1}{\partial y}=0=xe^u\frac{\partial u}{\partial y}+u+y\frac{\partial u}{\partial y} \Rightarrow \frac{\partial u}{\partial y}=\frac{-u}{xe^u+y} \\ \frac{\partial f_2}{\partial x} = 0 = 4xv+2x^2\frac{\partial v}{\partial x}+ y^2e^u\frac{\partial u}{\partial x} = \frac{\partial v}{\partial x}=\frac{-4xv+y^3e^u(\frac{e^u}{xe^u+y})}{2x^2}\\ \frac{\partial f_2}{\partial y} = 0 = 2x^2\frac{\partial v}{\partial y}+3y^2e^u+y^3\frac{\partial u}{\partial y}=\frac{\partial v}{\partial y}=\frac{-3y^2e^u+y^2(\frac{-u}{xe^u+y})}{2x^2} $$

Montamos então a matriz de diferencial e calculamos cada derivada no ponto $P=(x_0,y_0,u_0,v_0)=(1,1,0,0)$:

$$ Df_P = \begin{pmatrix} \frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} \\ \frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} \end{pmatrix} = \begin{pmatrix} -1/2 & 0 \\ 1/4 & -3/2 \end{pmatrix} $$

Resposta : e

Vamos escrever as frases em notação matemática. Seja $A$ o conjunto de alunos, e as propriedades:

• $P_i$ aluno estagiário
• $P_b$ aluno com bolsa
• $P_u$ aluno de último período

$$ \text{I.} \; \exists \; x \in A \;|\; P_i(x) \land P_b(x) \\ \text{II.} \; \forall x \in A \;|\; P_u(x) \land P_b(x) $$

Analisemos as respostas

• a) Incorreta. Nada foi dito sobre pelo menos um aluno do último período ser estagiário, ou seja, não se pode concluir isso das premissas.
• b) Incorreta. Podemos ter simultaneamente alunos de último período que fazem estágio.
• c) Correta. Essa combinação é permitida pelas afirmações.
• d) Incorreta. Podemos ter alunos do último período fazendo estágio, o que não podemos é ter todos fazendo estágio "com bolsa" ou ao menos um aluno do último período sem bolsa.
• e) Incorreta. Idem acima.

Sabendo que $n\rightarrow p$ deve ser verdade, $n$ só pode ser falso. Então, para que $m\rightarrow n$ seja verdade, $m$ é falso. Logo:

m	n	p	q	r	m->n	n->p	p->q	q->r
F	F	F	V	V	V	V	V	V

Das opções, a única correta é $n\rightarrow r$, ou, $F\rightarrow V$ é verdadeiro.

Resposta : a

Esse é um problema de combinação de 12 itens de 7 em 7 que pode ser resolvido por uma fórmula:

$$ C_{12,7}= \frac{12!}{7!(12-7)!}=\frac{12\cdot 11 \cdot 10 \cdot 9 \cdot 8 \cdot 7}{7!\cdot 5\cdot 4\cdot 3 \cdot 2}=792 $$

Resposta : b

Ainda não respondida.

Vamos transformar a proposição em notação matemática. Seja $S$ o conjunto de todas as sorveterias e $P_d$ a propriedade de um sorvete qualquer $s$ ser doce, sem adoçante.

$$ p=\exists \; s \; \in S \; | \; P_d(s) \\ \neg p = \forall s \in S | \neg P_d(s) $$

Que se traduz em: Para toda sorveteria, existe ao menos um sorvete que não é doce ou contém adoçante.

Resposta : d

Primeiro, coloquemos os conjuntos em ordem crescente:

$$ A=\{1,2,4,6,8,10 \} \\ B=\{1,4,6,10 \} \\ C=\{1,4,6,10\} \\ D=\{1,4,6\} $$

Disso já podemos concluir que:

• $B=C$
• $B,C,D\subset A$
• $B,C\nsubseteq D$

A resposta seria possivelmente o item d), mas a questão foi anulada.

Questão anulada

Esse é um problema de combinação entre cada categoria. Calculemos uma combinação de 6 farmacêuticos tomados 2 a 2 e 9 atendentes tomados 5 a 5, e multiplicamos os resultados:

$$ C_{6,2}=\frac{6!}{2!(6-2)!}=15 \\ C_{9,5}=\frac{9!}{5!(9-5)!}=126 \\ C_{6,2}\cdot C_{9,5}= 1890 $$

Resposta : c

Para calcular a probabilidade vamos precisar integrar $f(x)$ no intervalo dado, notando que antes precisamos garantir que a área embaixo da curva seja igual a 1.

$$ \int_{0}^1 k x^3dx=1 \Rightarrow \frac{kx^4}{4}|_0^1=1 \\ \Rightarrow k=4 $$

Agora podemos calcular a integral no intervalo dado:

$$ P(0,25 < x < 0,75)=\int_{0,25}^{0,75}4x^3dx\sim 0,3164 $$

Resposta : c

Para o primeiro presente posso escolher entre 35 turistas, porém, para o segundo, somente 34. Então, $35\cdot 34=1190$.

Resposta : e

Como a balança tem erro de 1 décimo, é melhor sempre pesar com o mínimo possível, assim, cada multiplicação gerará um erro pequeno. Dentre as opções, pesar 10 porções de 10 g é o caso de maior precisão.

Resposta : d

Questão anulada.

Ainda não respondida.

Questão anulada.

Como o algoritmo divide o arranjo de elementos em duas partes, a recursão é dita "binária". A recursão binária refere-se a um tipo específico de recursão em que uma função ou algoritmo se chama repetidamente a si mesmo, dividindo o problema em duas partes menores. Em vez de resolver o problema diretamente, a recursão binária divide-o em subproblemas menores e, em seguida, combina as soluções dos subproblemas para obter a solução geral.

Resposta : b

Questão anulada.

O limite superior é denominado de análise de pior caso, ou seja, dada uma entrada $n$, $T(n)$ será sempre menor do que $O(n)$.

Resposta : c

A travessia pré-fixada à esquerda em uma ABP implica em percorrer primeiro os nós da sub-árvore à esquerda do nó raiz e depois os nós à direita. Como o primeiro nó é 44, assumimos que esse é nó raiz, de forma que percorrer a árvore pelo outro lado implica que o primeiro nó também é 44. Só há uma resposta com esse padrão, que é a b.

Resposta : b

Começamos notando que o laço externo vai rodar para os valores $cont=\{4,5,6,7,8,9,10\}$, isto é, 6 vezes. O laço interno também rodará 6 vezes, para $k=\{7,6,5,4,3,2,1\}$. Vamos organizar os dados em uma tabela:

cont	k	i	j
4	7	0	-9
4	6	9	(6-9/2)=6-4=2
4	5	9	(5-2/2)=4
4	4	9	(4-4/2)=4-2=2
4	3	9	(3-2/2)=2
4	2	9	(2-2/2)=1
4	1	9	(1-1/2)=1
5	0	10	1
6	0	11	1
7	0	12	1
8	0	13	1
9	0	14	1
10	0	15	1

Resposta : b

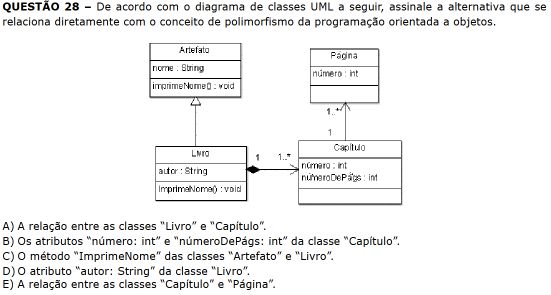
Polimorfismo permite que métodos comuns se comportem de maneira específica para cada classe, promovendo flexibilidade e reutilização de código. As duas únicas classes que tem métodos em comum são Artefato e Livro. No caso, Artefato é a classe base de Livro, sendo que a última deve sobrescrever o método $imprimeNome()$.

Resposta : c

Analisemos as afirmações:

I - Verdadeira. A RLE utiliza é adequada para longas sequências de caracteres que podem ser transformados em um padrão, por ex, AAAABBB = A4B3.

II - Verdadeira. A codificação de Huffman atribui códigos binários mais curtos para os símbolos mais frequentes e códigos mais longos para os menos frequentes.

III - Falsa. O método LZW (Lempel-Ziv-Welch) é um algoritmo de compressão de dados que visa reduzir o tamanho de arquivos ou dados por meio da identificação e substituição de sequências repetidas por códigos mais curtos.

IV - Verdadeira. Ver Teorema de Shannon.

Resposta : c

Transbordamento é conhecimento como "overflow" enquanto o mesmo fenômeno porém negativo é "underflow".

Resposta : d

Associatividade é a propriedade do operador que determina a precedência caso não existam parênteses para organizar os termos. Por exemplo: (5+2)-3 = 5+(2-3)

Resposta : a

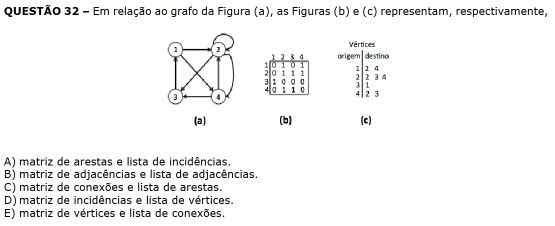
A figura b) representa a matriz de adjacências, que registra as conexões entre nós. Com isso só temos uma opção de resposta.

Resposta : b

1. Break - Termina a execução de um laço, continuando o programa na instrução imediatamente após o laço.

2. Continue - Faz com que uma iteração seja terminada, passando automaticamente à próxima iteração do laço.

3. Loop (infinito) - Apresenta uma condição de teste verdade que nunca termina o laço.

4. While - Executa uma instrução ou um bloco de instruções enquanto uma determinada condição for verdadeira.

O padrão é: 4 - 1 - 2 - 3

Resposta : d

Arquivo hash é um tipo de padrão de estrutura de dados usado para organizar arquivos em mídias secundárias (normalmente discos rígidos ou SSDs). Analisemos as afirmações:

A) Correta. Os buckets são unidades de armazenamento que ocupam um bloco inteiro em disco e possuem vários registros.

B) Correta. Quando o bucket transborda um novo é alocado para o mesmo hash e conectado ao anterior, chamado de hash fechado.

C) Correta. A indexação é o mecanismo utilizado para pesquisar registros com base no hash.

D) Incorreto. Hash extensível é o processo de aumentar dinamicamente um bucket através da produção de um grande número de valores, mas que só alguns são utilizados. Isso permite o controle de adicionar e remover registros sob demanda. Os bits utilizados na função hash permitem endereçar até 2n buckets.

E) Correta. Ver item anterior.

Resposta : e

Analisemos as afirmações.

I - Verdadeira. Organização de arquivos tipo "heap" é performática para inserção de um novo item porque o registro vai ao final do arquivo e não demanda operações de ordenação.

II - Falsa. Normalmente não faz comparação por igualdade, mas por algum trecho da busca para descartar nós que não tem relação com o item. Por exemplo, procurando por Ana em uma árvore ordenada, não precisamos analisar nós cuja raiz é a letra B.

III - Verdadeira.

IV - Falsa. Nesse caso deve-se ordenar o arquivo para poder utilizar a busca binária eficientemente.

Resposta : e

A resposta correta é a letra b). Quando o último nó do caminho tem um vértice para o primeiro, diz-se que o grafo é fechado.

Resposta : b

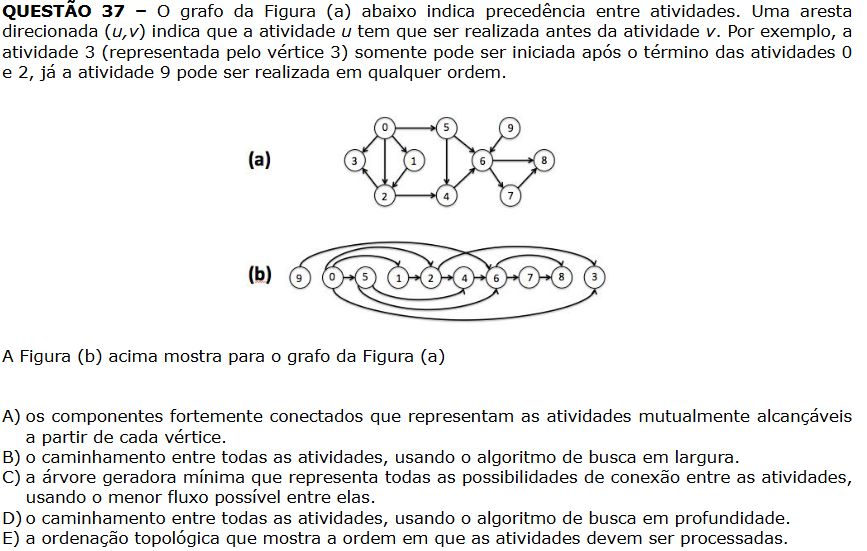
O gráfico representa uma ordenação topológica, que é um tipo de ordenação linear entre os vértices, mostrando transições de dependência.A principal aplicação da organização topológica está relacionada à representação e solução de problemas que envolvem dependências ou precedências.

Resposta : e

Ainda não respondida.

Ainda não respondida.

Ainda não respondida.

Ainda não respondida.

Ainda não respondida.

Ainda não respondida.

Ainda não respondida.

Ainda não respondida.

Ainda não respondida.

Ainda não respondida.

Ainda não respondida.

Ainda não respondida.

Ainda não respondida.

Precisamos esclarecer a terminologia utilizada. A pergunta versa sobre bancos de dados relacionais:

• Tupla: Um linha ou registro em tabela.
• Atributo: Cabeçalho de coluna ou propriedade.
• Relação: Uma tabela.
• Domínio: Tipos de dados de cada coluna.

V - Os registros não precisam ficar ordenados em uma tabela. Eles podem ser organizados pela consulta executada.

V - Os atributos são as colunas de uma tabela, que tem uma ordem específica obrigatória.

F - A chave primária não precisa ser o primeiro atributo. Esse é apenas uma boa prática.

Resposta : e

A presença de objetos que aparentam ter valores diferentes para usuários com diferentes passes (permissões) é chamada de Poli-Instanciação. Quando as tuplas podem ser armazenadas com nível de classificação maior e dela são produzidas tuplas correspondentes com nível menor, falamos do processo de Filtragem.

Resposta : c

O Gerenciamento de Configuração de Software (SCM - Software Management Configuration) é um processo utilizado para gerenciar, organizar e controlar alterações em itens de software, por exemplo, documentos, código fonte, imagens, diagramas, etc. O objetivo é implementar as melhores práticas para coordenar e sincronizar alterações nas entidades de software visando melhorias em produtividade e minimização de problemas de versionamento.

O primeiro passo é a produção ou planejamento de um documento de gerenciamento de configuração, que vai relacionar como registrar o que foi modificado, a motivação, por quem e quando (what, why, by whom e when). As mudanças assim podem ser rastreadas e revertidas, se for o caso. Com isso também é possível gerenciar os pacotes (releases) de atualização de um sistema, auxiliando em sua construção e manutenção.

Resposta : d

Uma porta de rede é um número de identificação associado a um processo específico ou serviço em um dispositivo. Quando os dados são transmitidos em uma rede, eles são encapsulados em pacotes que incluem informações sobre a origem, o destino e outras informações relevantes. A porta de rede é um elemento-chave dessas informações, permitindo que o roteador ou comutador encaminhe os pacotes para a aplicação ou serviço correto.

Resposta: a

Vamos montar uma tabela com os registros informados.

at1	at2	at3
12	15	5100
13	NULL	3500
14	NULL	NULL
15	12	NULL

A consulta C1 retorna os 4 registros da tabela com a primeira condição. A segunda só é verdade pro primeiro item. Então, só deve retornar uma linha.

A consulta C2 retorna uma linha para a primeira condição e duas para a segunda. Então, deve retornar duas linhas.

A consulta C3 só deve retornar o último registro, que tem at1 (15) maior do que at2 (12).

Resposta : d

Devemos usar as informações de cada item para responder a pergunta. Começando dos dois últimos é mais fácil:

I -Diagrama de implantação.

II - Diagrama de Componentes

III - Diagrama de sequência

IV - Diagrama de Pacotes

Resposta : c

As três afirmações são verdadeiras.

I - Um exemplo do que é o Window (janela) e o ViewPort abaixo.

Fonte: Geeks for Geeks

Nas coordenadas mundo, selecionamos uma área, que é a janela, com coordenadas $(x_{min}, y_{min})$ e $(x_{max},y_{max})$.

II - A transformação entre window e viewport exige um redimensionamento do tamanho da imagem que será exibida no dispositivo escolhido. Aplica-se uma normalização da relação entre os pontos da janela e também da viewport. Sejam $(x_w,y_w)$ um ponto da janela e $(x_v, y_v)$ um ponto correspondente na viewport:

$$ x_v = x_{vmin}+(x_w+x_{wmin})S_x \\ y_v = y_{vmin}+(y_w+y_{wmin})S_y \\ $$

Onde $S_j$ é o fator de escala. Um exemplo pode ser visto em: Window to Viewport Transformation in Computer Graphics with Implementation.

III - Clipping é o processo de decidir qual parte da imagem gerada será utilizada para exibição no dispositivo (viewport).

Resposta : e

O volume de visão em projeção perspectiva refere-se ao espaço tridimensional que é capturado e visualizado em uma cena quando representada em uma imagem bidimensional usando a técnica de projeção perspectiva. Em outras palavras, é o intervalo de espaço que pode ser visto a partir de um determinado ponto de observação e que será projetado na imagem final.

Resposta : b

I - É uma técnica utilizada para manipular a forma e estrutura de objetos em uma imagem.

II - A amostragem envolve a redução da resolução de uma imagem, selecionando um subconjunto de pixels para representá-la. Isso é feito para reduzir o tamanho do arquivo ou ajustar a imagem a um espaço limitado. A quantização, por outro lado, envolve a redução do número de tons de cor ou níveis de intensidade em uma imagem.

III - A segmentação é a técnica de dividir uma imagem em regiões ou segmentos significativos com base em características como cor, textura, intensidade ou bordas. O objetivo é simplificar a análise e o processamento, facilitando a identificação de objetos e regiões de interesse em uma imagem.

IV - (Simulated Annealing) É uma técnica de otimização combinatória utilizada em inteligência artificial para encontrar soluções aproximadamente ótimas para problemas complexos.

V - É um método para segmentação de imagens que pode ser usado em um processo de binarização. Essa técnica é frequentemente usada para realçar características específicas em imagens, como bordas ou objetos de interesse.

Resposta : d

ARP (Protocolo de resolução de endereço) é responsável por resolver o problema de tradução entre endereços IP (Internet Protocol) e endereços MAC (Media Access Control), que são usados em diferentes camadas do modelo de referência OSI.

Quando um dispositivo precisa enviar dados para outro dispositivo em uma rede, ele usa o endereço IP do destino. No entanto, os dispositivos utilizam os endereços MAC para a comunicação direta dentro da mesma rede. O ARP entra em cena para traduzir o endereço IP em um endereço MAC correspondente, possibilitando a entrega adequada dos pacotes.

Resposta : e

"A transformada wavelet direta mapeia os dados da imagem original para um outro domínio, sem fornecer nenhuma compressão dos dados em relação a imagem original, porém a transformada inversa, em muitos casos, permite uma reconstrução exata das informações anteriores.". (Sanches, 2003, p.15) Ela se baseia na matemática das transformadas wavelet, que permitem a decomposição de uma imagem em diferentes escalas e frequências, oferecendo uma visão detalhada e abrangente das características da imagem. O conceito de multiresolução permite a construção de novas bases de wavelets e uma interpretação invariante de escala da imagem, ou seja, quando mudamos sua escala a interpertação continua a mesma.

Resposta : b

O método publicar-assinar, também conhecido como publish-subscribe (ou pub-sub), é uma abordagem fundamental em sistemas distribuídos que permite a comunicação assíncrona eficiente e escalável entre diferentes componentes ou nós. Esse método é amplamente utilizado em ambientes onde múltiplos participantes precisam trocar informações sem a necessidade de conhecimento direto uns dos outros.

Resposta : b

Durante a representação intermediária não é necessário saber qual a máquina-alvo. Esse processo é necessário ao gerar o código de máquina. A principal função da representação intermediária é fornecer uma forma mais simplificada e padronizada do código-fonte original, tornando mais fácil a análise, transformação e otimização. Ela é criada durante a etapa de análise sintática e semântica do compilador, quando o código-fonte é analisado e estruturado em uma forma mais compreensível para a máquina.

Resposta : d

A transparência de acesso em sistemas distribuídos é um conceito fundamental que busca ocultar a complexidade subjacente da comunicação e do acesso a recursos distribuídos, oferecendo aos usuários e aplicativos uma visão unificada e simplificada do ambiente distribuído. Em outras palavras, a transparência de acesso visa tornar a interação com sistemas distribuídos tão transparente e natural quanto a interação com um sistema centralizado.

Resposta : a

Ethernet é uma família de tecnologias de rede de computadores com fio comumente usadas em redes de área local (LAN), redes de área metropolitana (MAN) e redes de longa distância (WAN). (Wikipédia) Ele define as especificações para a transmissão de dados em uma rede, incluindo o formato dos quadros, a velocidade de transmissão e os métodos de acesso ao meio.

Em algumas implementações, especialmente em redes TCP/IP, o controle de congestionamento pode ser influenciado pela janela de congestionamento do protocolo TCP.

Resposta : b

Filtros de transformação espacial, também conhecidos como filtros de convolução ou máscaras de convolução, são uma técnica essencial no processamento de imagens. Eles são utilizados para realçar, suavizar, detetar bordas e outras operações em imagens digitais, com base em operações matemáticas aplicadas a regiões locais da imagem.

Resposta : d

As únicas afirmações corretas são I e II.

III - Em comunicação síncrona o remetente deve aguardar pelo retorno do destinatário da mensagem antes de continuar.

IV - Aqui ocorre o contrário, o destinatário entrega a mensagem e pode continuar seu processamento sem aguardar o retorno do destinatário.

Resposta : a

Apenas a assertiva I está correta.

II - A informação de linha e coluna não é usada.

III - As notações para identificação dos lexemas estão na gramática da linguagem.

IV - A representação intermediária é gerada em outro processo do compilador.

Resposta : a

O termo "aprendizado de máquina" refere-se a um campo da inteligência artificial (IA) que se concentra no desenvolvimento de algoritmos e modelos que permitem que as máquinas aprendam a partir de dados. Em vez de serem explicitamente programadas para executar tarefas específicas, as máquinas aprendem com exemplos e experiências, ajustando seus modelos internos para melhorar o desempenho em tarefas futuras.

Resposta : b

Os requisitos não-funcionais de implementação se referem à maneira como o sistema é projetado, construído e organizado internamente. Eles estão relacionados à estrutura do código-fonte, à arquitetura do sistema, à escolha de tecnologias e às práticas de codificação.

Os requisitos não-funcionais de portabilidade referem-se à capacidade do sistema de ser executado em diferentes ambientes, plataformas ou dispositivos sem modificações significativas.

Os requisitos não-funcionais de interoperabilidade tratam da capacidade do sistema de se comunicar e interagir com outros sistemas ou componentes de software. Isso é particularmente importante em ambientes onde várias soluções precisam colaborar para cumprir os objetivos do usuário ou do negócio.

Resposta : d