I. Podemos calcular a equação:

$$ Av=\lambda v $$

e encontrar que não há valor de $x$ que resolva o sistema de equação para encontrar $\lambda$. Esse item é incorreto.

II. Podemos calcular o polinômio característico pela equação $det(A-\lambda I)$ e encontrar que os autovalores são diferentes do apresentado. Item incorreto.

III. Basta calcular a inversa através da operação

$$ A^{-1} =\begin{bmatrix} 2 & 1 & 0 & | & 1 & 0 & 0 \\ 1 & 0 & 2 & | & 0 & 1 & 0 \\ 0 & 2 & 1 & | & 0 & 0 & 1 \\ \end{bmatrix} $$

ou seja, a matriz do lado esquerdo deve virar a matriz identidade e a do lado direito será a inversa de $A$. Com isso verás que o item é correto.

IV. Existe um teorema que relaciona o polinômio minimal $m(t)$ com o característico $p(\lambda)$, ou seja, há um $m_i(\lambda)=p(\lambda)$. Se $p(\lambda)=-\lambda^3+3\lambda^2+3\lambda-9$ então devemos encontrar as raízes $3, \sqrt{3}, -\sqrt{3}$. Logo um polinômio que divide $p(\lambda)$ é $(\lambda-3)$, calculamos o polinômio resultante e verificamos que somente $p(A)=0.$

Resposta: c

Primeiro analisamos os vetores normais de cada equação:

$$ v_1=[3\;1\;1]\\ v_2=[5\;3\;2]\\ v_3=[7\;7\;8] $$

Claramente os vetores são linearmente independentes e isso já nos diz que não planos paralelos ou coincidentes. Devemos resolver o sistema para avaliar o cruzamento dos três planos. Obtemos $x=0,y=1,z=1$, ou seja, encontram-se somente em um ponto.

Resposta: e

Questão anulada.

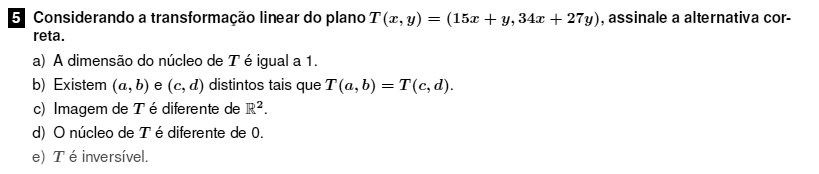
Para verificar se a dimensão do núcleo, devemos achar $ker(T)={\{(x,y)\;|\; T(x,y)=0 \}}$. Para isso resolvemos o sistema:

$$ 15x+y=0\\ 34x+27y=0\\ x=0, y=0 $$

Como o único vetor é $w=(0,0)$, não há base para $ker(T)$, então sua dimensão é zero. O item a) está incorreto.

Como $T(a,b)=T(c,d)$, temos que

$$ T(a,b)=(15a+b,34a+27b)\\ T(c,d)=(15c+d,34c+27d)\\ 15a+b=15c+d\\ 34a+27b=34c+27d $$ onde temos um sistema com 2 equações e 4 incógnitas, que não pode ser resolvido. Então, item falso.

Pelo item a), sabemos que $dim(ker(T)=0$, pelo Teorema Núcleo-Imagem

$$ dim(\mathbb{R}^2)=dim(ker(T)+dim(Im(T)) \\ 2=0+dim(Im(T) \\ dim(Im(T))=2 $$

Logo, item incorreto.

Como vimos em a), também, o núcleo de T só contém o vetor $0=(0,0)$. Item incorreto.

Sabemos que e) é a resposta correta. Basta aplicar algum método de inverter T, em forma de matriz, e obter o resultado correto.

Resposta: e

a) Sejam $u,v \in \mathbb{R}^3$. O produto de vetores é dado por:

$$ u=[u_1 \;u_2\;u_3], v=[v_1\;v_2\;v_3]\\ u\times v= \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \\ \end{vmatrix} \ne v\times u $$

ou seja, $u\times v= -v\times u$. Item incorreto.

b) A propriedade associativa não vale para produto vetorial pelo mesmo motivo do item a), isto é, $u\times (v\times w) \ne (u\times v)\times w.$

c) As matrizes não são comutativas. Ver item a).

d) A propriedade distributiva nos diz que: $u\times(v+w)=(u\times v)+(u\times w)$ que vale. Item correto.

e) Se $u\times v=0$ , temos novamente um determinante com os vetores ortonormais na primeira linha. Um contra exemplo é o caso em que $u=(1,0,0)$ e $v=(0,1,0)$. O produto vetorial é zero, mas eles não são nulos. Item incorreto.

Resposta : d

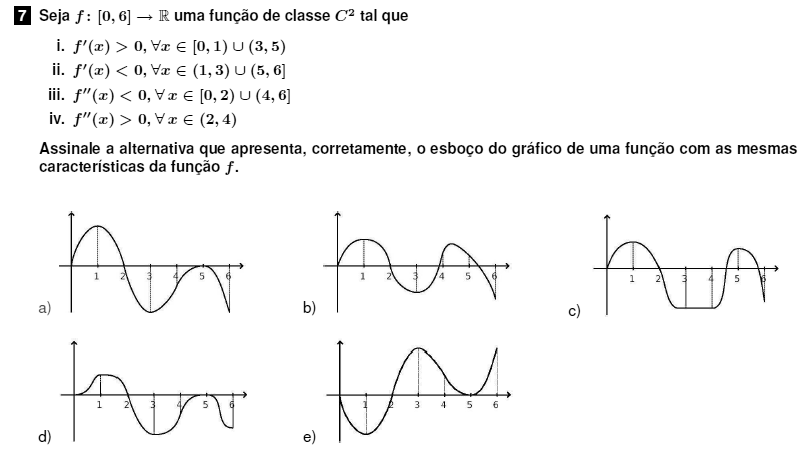
Sabendo que a função possui as duas derivadas por ser do tipo $C^2$, analisemos os intervalos pela primeira derivada $f'$:

$[0,1)$ - Os valores de $f$ devem crescer;

$(1,3)$ - Os valores da função estão decrescendo;

$(3,5)$ - Os valores da função estão crescendo;

$(5,6]$ - Os valores da função estão decrescendo.

Agora do ponto de vista de $f''$:

$[0,2)$ - A taxa de crescimento vai diminuindo;

$(2,4)$ - A taxa de crescimento vai aumentando;

$(4,6]$ - A taxa de crescimento vai diminuindo.

A partir da análise acima concluímos que $f$ vai crescendo com taxa de crescimento entre $[0,1)$ e $(3,5)$ e vai decaindo entre $(1,3)$, cada vez menos, assim como em $(5,6]$. Logo, a resposta é o item a).

Resposta : a

Temos dois vetores no conjunto $B$:

$$ \vec{u}=(1,2) \\ \vec{v}=(3,4) $$

A primeira afirmação nos diz que $\vec{u}$ e $\vec{v}$ são uma base, ou seja, devem ser linearmente independentes (L.I.). Podemos escrever essa restrição como uma combinação linear, e avaliar sua solução:

$$ \vec{v}=\alpha \vec{u}=\alpha (1,2) \\ 3=1\alpha \\ 4=2\alpha $$

De forma que não existe um $\alpha$ que satisfaça as equações acima. Logo, a afirmação I é verdadeira.

A afirmação II nos diz que bases só possuem coordenadas 0 ou 1, o que é falso. Para ser uma base, como dito na resposta anterior, basta que os vetores sejam L.I. Então, afirmação falsa.

Podemos checar a afirmação III olhando para o ângulo entre os vetores. Isso pode ser feito pela equação:

$$ cos(\theta)=\frac{\vec{u}\cdot\vec{v}}{|\vec{u}|\cdot |\vec{v}|}=\frac{3+8}{\sqrt{5}+5}\ne 0 $$

Logo, os vetores da base não são ortogonais. Afirmação III incorreta.

Afirmação IV: Se $w=\frac{1}{\sqrt{5}}(1,2)$ e $k=\frac{1}{\sqrt{5}}(2,-1)$, então:

$$ |\vec{w}|=\frac{1}{\sqrt{5}}\sqrt{1+4}=1 \\ |\vec{k}|=\frac{1}{\sqrt{5}}\sqrt{4+1}=1 $$

Onde provamos que são normalizados. Para ortogonalidade, temos que calcular $u_i \in B \cdot v_j \in C$, mas antes temos que normalizar os vetores em $B$:

$$ \hat{u}=\frac{\vec{u}}{|\vec{u}|}=\frac{(1,2)}{\sqrt{5}}\\ \hat{v}=\frac{\vec{v}}{|\vec{v}|}=\frac{(3,4)}{5}\\ $$ $$ \hat{u}\cdot \vec{w}=\frac{1}{5}(1+4)=1\\ \hat{u}\cdot \vec{k}=\frac{1}{5}(2-2)=0\\ \hat{v}\cdot \vec{w}=\frac{1}{5\sqrt{5}}(3\cdot 1+4\cdot 2)=\frac{11}{5\sqrt{5}}\\ \hat{v}\cdot \vec{k}=\frac{1}{5\sqrt{5}}(6-4)=\frac{2}{5\sqrt{5}}\\ $$

Essa afirmação parece incorreta também. Essa questão deveria ter sido anulada, mas a resposta do gabarito é a letra b).

Se $\vec{t}$ é L.I. de $\vec{a}$ e $\vec{b}$, então, não existe uma combinação linear de $\vec{a}$ e $\vec{b}$ que possa gerar $\vec{t}$. Disso excluímos a resposta d).

Nada foi dito da reta $t$ estar no plano $\alpha$, então a resposta c) está incorreta.

A e) é incorreta porque podemos gerar $-\vec{t}$ a partir de $\vec{t}$.

A b) também está incorreta porque não podemos dizer que qualquer reta do plano $\alpha$ seja paralela à $\vec{t}$.

Portanto, a resposta correta é a letra a).

Resposta : a

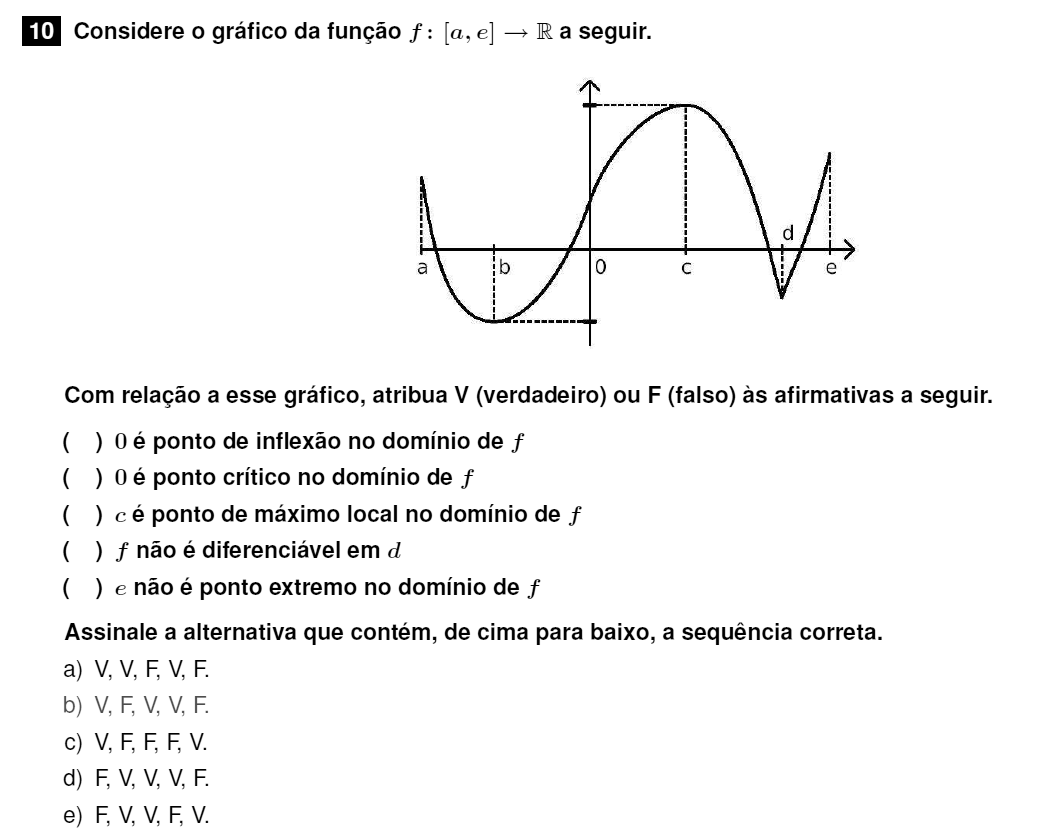
Um ponto de inflexão ocorre quando há mudança de concavidade e a segunda derivada muda de sinal. Isso ocorre no ponto (0,0). Primeiro item é verdadeiro.

Um ponto crítico ocorre quando a derivada é zero ou indefinida. Isso não ocorre no ponto (0,0). Segundo item falso.

O ponto c é um máximo local e global da função no intervalo. Esse item é verdadeiro.

O ponto d está definido para a função no intervalo, porém, não é diferenciável porque a curva não é "suave", ou seja, nas redondezas de d não podemos determinar a reta tangente para calcular a derivada de f(d). Item falso.

Um ponto extremo é um máximo ou mínimo local. Já vimos que c é um máximo global. Item falso.

Resposta : b

Em linguagem simbólica, a frase dada é escrita como: $P\rightarrow Q$, ou seja, se P então Q. A negação é dada por

$$ \neg(P\rightarrow Q)=\neg P \lor \neg Q $$

Entretanto, precisamos encontrar uma resposta equivalente para obter o resultado desejado. Vamos reescrever a relação original como: $P\rightarrow Q=\neg P \lor Q$. Agora negamos: $\neg(\neg P \lor Q)$, e, aplicando a lei de De Morgan, temos:

$$ \neg(\neg P \lor Q)=P\land \neg Q $$

Resposta : c

Na letra a), $X_{4+1}=4\cdot X_4$, onde

$$ X_1=1\\ X_{1+1}=1\cdot X_1 = 1 \\ X_{2+1}=2\cdot X_2 = 2 \\ X_{3+1}=3\cdot X_3 = 6 \\ X_{4+1}=4\cdot X_4 = 24 $$

Então, $X_5=24$. Item incorreto.

Usando a mesma estratégia do item anterior:

$$ X_1=3\\ X_{1+1}=1\cdot X_1 = 3 \\ X_{2+1}=2\cdot X_2 = 6 \\ X_{3+1}=3\cdot X_3 = 18 \\ $$

$3!\cdot 3= 3\cdot 2\cdot 1 \cdot 3 = 18$. Item correto.

Resposta : b

Afirmação I. Pela tabela verdade $P \updownarrow Q = F$, mas não temos uma relação de equivalência definida, ou seja, se $P \updownarrow Q = F$ então $Q \updownarrow P = F$. Logo essa afirmação está incorreta.

Afirmação II. Uma contingência ocorre quando uma proposição composta não é uma tautologia nem contradição, isto quer dizer que o resultado da proposição composta só depende dos valores lógicos das proposições simples. Neste caso, é uma contigência porque precisar avaliar $P \updownarrow Q$ e $Q \updownarrow P$. Item incorreto.

Afirmação III. Uma contradição ocorre sempre que uma proposição composta é falsa, independente dos valores das proposições mais simples que a compõem. Podemos avaliar os casos que temos:

$$ (V \updownarrow F) \land (F \updownarrow V)=F \\ (V \updownarrow V) \land (V \updownarrow V)=F \\ (F \updownarrow V) \land (V \updownarrow F)=F \\ (F \updownarrow F) \land (F \updownarrow F)=F $$

Ou seja, é uma contradição. Afirmação correta.

Afirmação IV. Uma tautologia ocorre quando uma proposição composta é sempre verdadeira, independente dos valores das proposições mais simples que a compõem. Vamos avaliar primeiro a proposição composta

$$ \neg [(Q \updownarrow P) \lor (P \updownarrow Q)] \\ [\neg (Q \updownarrow P) \lor \neg (P \updownarrow Q)] \\ $$

Os casos estão são:

$$ \neg (V \updownarrow F) \lor \neg (F \updownarrow V)=V \\ \neg (V \updownarrow V) \lor \neg (V \updownarrow V)=V \\ \neg (F \updownarrow V) \lor \neg (V \updownarrow F)=V \\ \neg (F \updownarrow F) \lor \neg (F \updownarrow F)=V $$

que é uma tautologia. Item correto.

Resposta : c

Questão anulada.

Vamos definir as proposições simples:

P=Daniel treina nas aulas de tênis.

Q=Daniel será um grande tenista.

R=Daniel come alimentos saudáveis.

A sentença inicial é dada pela proposição composta:

$$ P \rightarrow Q $$

ou seja, se $P$ então $Q$. A segunda parte é dada por:

$$ P \land R $$

que não afeta Q. Vamos analisar as respostas:

a) Incorreta. A conclusão não vem das premissas.

b) Incorreta. Idem acima.

c) Incorreta. Dissemos que R não afeta Q e se P então Q.

d) Incorreta. A premissa é se P então Q.

e) Correta. A conclusão tem como base a premissa $P \rightarrow Q$.

Resposta : e

Afirmação I. A propriedade comutativa implica que $\forall x,y \in S, x@y = y@x$. Para verificarmos essa propriedade na tabela da operação, basta olharmos os números nas diagonais da esquerda pra direita, que devem ser simétricas. Veja imagem abaixo:

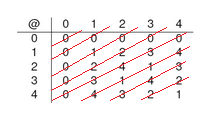
Logo, a propriedade é verificada. Item correto.

Afirmação II. Usando o mesmo argumento do item anterior, temos que a propriedade é verificada para a operação # em $S$. Item correto.

Afirmação III. O elemento neutro é tal que $\forall x \in S, x\#0 = x$. Para verificarmos isso, basta olharmos a segunda coluna da tabela de # e notar que ela é igual à primeira coluna, ou seja, qualquer elemento de $S$ operando com # dá ele mesmo. Item correto.

Afirmação IV. O elemento inverso é tal que $\forall x \in S, x@1=0$, onde 0 é o elementro neutro. Notamos na tabela que esse não é o caso, como, por exemplo, $2\#1=2 \ne 0$. Item incorreto.

Resposta : d

Como não há diferença entre as bolas de mesma cor, temos uma permutação com repetição:

$$ P_{12}^{7,5}=\frac{12!}{7!5!}=792 $$

Resposta : b

A chance de não sair um 2 é $P_{\ne 2}=5/6$, que é a mesma chance para o número 5, $P_{\ne 5}=5/6$. Não sair um dos dois é o mesmo que sair qualquer um dos outros quatro números {1,3,4,5}. Então, $P_{~2,5}=\frac{4}{6}=\frac{2}{3}$

Resposta : e

Uma partição de $A$ é qualquer subconjunto formado com elementos de $A$, escrito como $\mathcal{P}(A)$. Todo elemento de $A$ deve estar contido ao menos uma vez em algum subconjunto de $\mathcal{P}(A)$.

Afirmação I. Incorreto. A partição não contém o conjunto vazio.

Afirmação II. Incorreto. Vide anterior.

Afirmação III. Correto. Todos os elementos de $A$ aparecem ao menos uma vez nos subconjuntos de $\mathcal{P}(A)$.

Afirmação IV. Correto. Idem item anterior.

Resposta : c

A média pode ser calculada como:

$$ S=\frac{1}{n}\sum_i^n i=\frac{72}{12}=6 $$

A moda é o valor que mais se repete no conjunto. Neste caso é 8. A mediana é o valor que divide o conjunto entre duas partes iguais. Como temos um número par de itens, será a média entre os itens do meio, no caso, $\frac{5+5}{2}=5$.

A resposta é: ME < MA < MO

Resposta : d

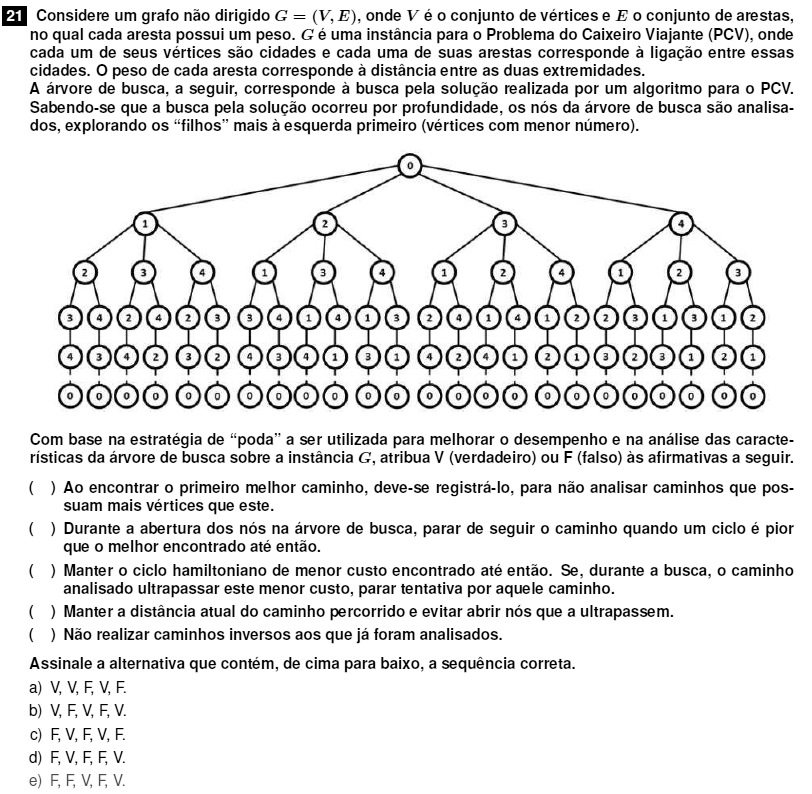
O Problema do Caixeiro Viajante (TPS - Travelling Salesperson Problem) é muito estudado em Ciência da Computação por sua complexidade na relação entre o número de vértices do grafo $G$ e as restrições dadas para escolher o melhor caminho. Ele pode ser transformado em um problema de otimização para ser resolvido utilizando programação linear. É um problema dito NP-Difícil.

A primeira afirmação, que chamaremos de i), diz que não devemos analisar caminhos com mais vértices do que aquele melhor já encontrado. Isso é falso porque não necessariamente um caminho com mais vértices é pior. Temos que analisar os pesos.

ii) Se pararmos ao encontrar um ciclo pior não sabemos se há outro melhor em frente. Item falso.

iii) Um ciclo hamiltoniano é uma trilha (nenhuma aresta é repetida). Se a soma atual das arestas é maior do que o registrado, esse caminho não tem como ser reduzido, então deve-se parar e tentar outro. Item verdadeiro.

iv) Um caminho ou caminhada é uma sequência de vértices e arestas, que podem ser repetidos. Se em um determinado caminho, $i$, a soma dos pesos deu $d_i$, a afirmação nos diz que não deveríamos abrir caminhos $j$, onde $d_j > d_i, j\ne i$. Isso é incorreto pois não sabemos se até o fim do ciclo os dois caminhos terão a mesma distância. Item falso.

v) Se a distância de A até B for a mesma do que B até A, então não precisamos avaliar o caminho inverso. Item verdadeiro.

Resposta: e

I) Verdadeiro. Armazenamento contíguo implica que cada arquivo ocupa o espaço imediatamente posterior a outro na memória, então, para acessá-los, deve-se marcar o começo do bloco e então, com o tamanho de cada um, pode-se acessar todos os outros.

II) Verdadeiro. É bem rápido de ser acessado porque basta pegar o primeiro bloco e somar o tamanho dos arquivos subsequentes para chegar onde se deseja.

III) Verdadeiro. Como comentado antes, acessar um arquivo de forma aleatória é não precisar passar por outros antes. Neste caso isso é excelente para o desempenho.

IV) Falso. Acesso contíguo tem o problema de alocar tamanhos arbitrários de arquivos em sequência, causando “buracos” no espaço em disco, ou seja, fragmentação.

Resposta: d

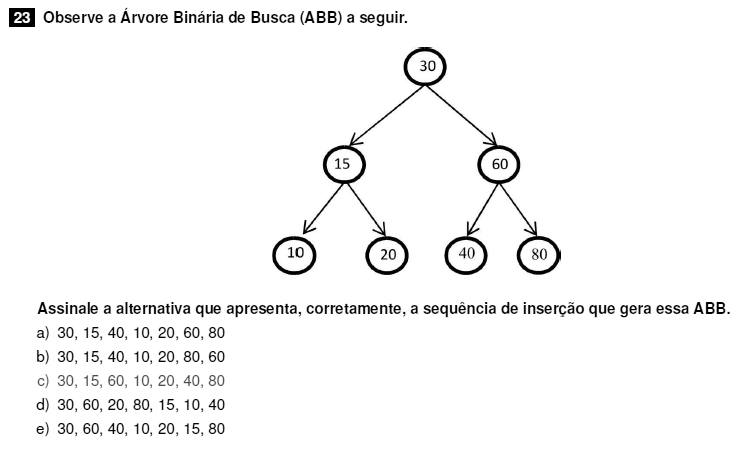
Devemos observar que uma árvore binária tem no máximo 2 filhos em cada nó e deve ser preenchida como uma busca em largura: de nível em nível. Neste caso, o primeiro nível é a raiz. Depois temos os nós 15 e 60. Depois os filhos de 15, 10 e 20 e por último os filhos de 40 e 80.

Resposta: c

I) Correta. Uma lista encadeada tem sempre um primeiro elemento que aponta para o próximo, é praticamente sua definição (faltam apenas as operações e o valor).

II) Correta. Para acessar um elemento no meio de uma lista com 100 itens, você deve passar por todos os anteriores pois não há acesso direto nesta estrutura.

III) Incorreta. Não existe essa restrição de blocos de dados para lista encadeada.

IV) Incorreta. Deve-se armazenar também um ponteiro para o próximo arquivo.

Resposta: a

a) Errada. Empilhamento e desempilhamento são operações da estrutura de pilha. Não vale para todos. Impressão não é uma operação básica.

b) Errada. Impressão não é uma operação básica.

c) Correta. Inicializar, inserir e remover são as operações básicas em um TAD.

d) Errada: Impressão não é uma operação básica.

e) Errada: Inserir em um ponto e remover todos não são operações básicas.

Resposta: c

Questão anulada.

I) Correto. Programação funcional tem como principal diferencial o uso de funções matemáticas para criar programas, onde não há mudanças de estados (efeitos colaterais) nem laços. O programador deve usar recursão para tratar de iterações. Lisp e Erlang são exemplos.

II) Incorreta. Programação imperativa utiliza declarações para mudar o estado de objetos no programa.

III) Incorreta. A programação orientada à objetos é muito útil na modelagem de problemas reais, justamente por suas características de abstração e herança.

IV) Correto. Ao invés de lidarmos com fluxos de controle, utilizamos expressões lógicas através de proposições. Exemplo: Prolog.

Resposta: b

I) C : char, int, float, double.

II) C# : char, int, bool, float, double

III) Java: char, int, boolean, float, double

IV) Pascal : char, boolean, integer, real

V) VisuAlg : caracter, logico, inteiro, real

Resposta : e

I) Correto. Exemplo, ao compararmos dois números, var1 == var2, precisamos garantir que os tipos são compatíveis, isto é, em linguagens tipadas, não faz sentido comparar um tipo booleano com um inteiro sem fazer uma conversão. Se a linguagem já avalia corretamente que um int pode ser comparado com um float, então a conversão é direta.

II) Incorreta. Os dois são importantes, mas o erro da afirmação é dizer que a prioridade é dada à semântica do programa. O processo de compilação tem várias fases.

III) Incorreta. É possível fazer a validação de tipos em tempo de execução, bastando avaliar o lado direito da atribuição para tal. Exemplo: variavel = “char” ⇒ variavel é string.

IV) Correto. Vinculação dinâmica exige identificar qual o tipo através do valor atribuído à variável e deve ser feito em tempo de execução pois o compilador não sabe qual tipo utilizar (late binding).

Resposta: b

É importante notar no código que somar sem atribuição não muda a variável envolvida. Quando somamos + 1 no printf, o valor da variável myCount continua em zero, apesar de aparecer 1 na tela de comando. Desta forma, ela nunca chegará até 10 e o programa vai rodar infinitamente.

Resposta: e

V) C++ nasceu do C, implementando orientação à objetos como característica principal.

F) Java é compilada, assim como C++.

V) A linguagem java possui os comandos try / catch para tratar exceções.

F) Possuem tipagem estática, isto é, os tipos devem ser definidos para cada variável.

V) No Java não é necessário se preocupar com liberação de memória de variáveis, o garbage collector se encarrega disso. No C++ o programador precisa alocar e desalocar as variáveis manualmente.

Resposta: b

a) Incorreta. O ponteiro foi declarado corretamente, não há erro de sintaxe.

b) Incorreta. Não há erros no laço de repetição. O ponteiro tem o endereço da variável e o operador unário * recupera o seu valor.

c) Incorreta. Vai exibir os valores do endereço indicado pela operação $(p+i)$ no printf.

d) Correta. Ambos os códigos vão imprimir a matriz $2\times 2$.

e) Incorreta. As declarações são válidas na linguagem C para uma matriz multidimensional.

Resposta : d

O algoritmo mergesort utiliza recursão para ir dividindo uma lista pela metade até sobrar apenas um item de cada parte. A operação de recursão tem complexidade $O(log(n))$ e é executada $n$ vezes, resultando em $O(n\cdot log(n)).$

Resposta: b

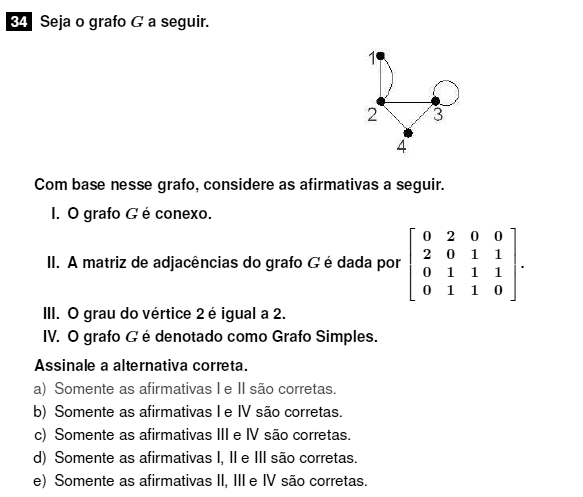
I) Correto. Um grafo é dito conexo se há caminho entre quaisquer pares distintos de vértices, isto é, partindo de qualquer um podemos chegar em outro.

II) Correto. A matriz exibe as relações entre os nós, nas linhas vamos de 1 até 4, assim como nas colunas. Um elemento $M_{ij}$ relaciona o item $i$ com o $j$, ou seja, se há ou não um vértice entre eles. Exemplo: $M_{33}=1$ pois há um vértice loop apontando de 3 para ele mesmo.

III) Incorreto. Há 4 vértices conectados ao nó 2.

IV) Falso. Um grafo é dito simples se não há vértices paralelos ou loops.

Resposta: a

Um conjunto é dito fechado para uma operação se o resultado dela leva a um elemento do próprio conjunto. Por exemplo, a operações de soma é fechada nos naturais pois quaisquer dois números somados resulta em um número natural. Nas linguagens livres de contexto, as operações de concatenação, homomorfismo (operação que preserva a estrutura algébrica) e reverso são fechadas.

Resposta: c

I) Correta. O heapsort tem uma performance muito boa mesmo nos piores casos (próxima da média).

II) Correta. O insertion sort trabalha com dois loops aninhados para encontrar a posição de cada elemento, um a um. É rápido para vetores pequenos ou já ordenados, mas tem complexidade no pior caso de $O(n^2)$.

III) Correta. O quick sort tem complexidade no geral $O(nlogn)$ e é parecido com o merge sort, mas utiliza um elemento pivô para quebrar o vetor em partes menores.

IV) Incorreta. O bubble sort tem complexidade $O(n^2)$ e normalmente é mais ineficiente que os outros métodos, fazendo várias passagens pelo vetor para comparação dois a dois dos elementos.

Resposta: d

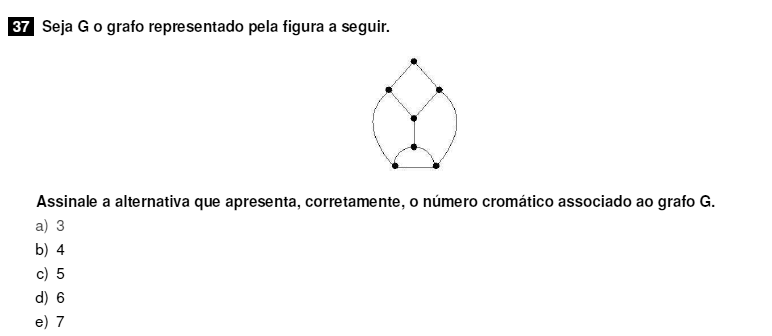
O número cromático diz respeito ao menor de cores utilizadas para colorir o grafo, sendo que dois elementos adjacentes tenham cores distintas. Dividindo o grafo em quatro partes, vemos que três delas sempre estão em contato, ou seja, precisamos de ao menos 3 cores únicas nesse caso.

Resposta: a

O lema do bombeamento permite mostrar que certas linguagens não são regulares, isto é, permite analisar que certas cadeias formadas por símbolos da linguagem (palavras) podem ser repetidas indefinidamente e ainda assim formarem uma palavra aceita. Uma linguagem é dita regular se é pode ser implementada utilizando-se expressões regulares, ou seja, é um tipo mais simples de linguagem que pode ser desenvolvida por algoritmos de reconhecimento.

I) Incorreto. A regra para gerar uma palavra, $w\in \Sigma^*$ onde $w$ termina com $b$ não é válida para o Lema, já que o trecho a ser repetido está entre dois símbolos $aw^ib$.

II) Correto. Com $n\geq1$, podemos gerar palavras do tipo $aa, aaa,aaaa,aaaaa,...$ de forma que qualquer um desses também é uma palavra.

III) Correto. Da mesma forma que o item acima, podemos gerar nos três casos elementos com símbolos nas bordas que podem ser repetidos ad infinitum e ainda sim serão elementos da linguagem $\Sigma.$

IV) Correto. Linguagens do tipo 3 são as regulares.

Resposta : e

I) Correto. A programação dinâmica é uma forma de abordar problemas que tem subproblemas que, quando sobrepostos, remontam o problema original. Quando obtemos uma solução para o problema, também encontramos a solução para subproblemas deste enquanto a sobreposição ocorre sempre que o algoritmo recursivo passa várias vezes por uma mesma operação.

II) Incorreto. A solução recursiva pode ser implementada para tentativa e erro, mas deve-se avaliar a complexidade espacial e os casos de parada para evitar problemas de performance.

III) Incorreto. Um algoritmo iterativo pode ter solução mais rápida que o recursivo, além de economizar espaço em memória.

IV) Correto. A estrutura de dados em árvore é ótima para utilização da recursão pois repete determinados padrões em qualquer nó avaliado.

Resposta: b

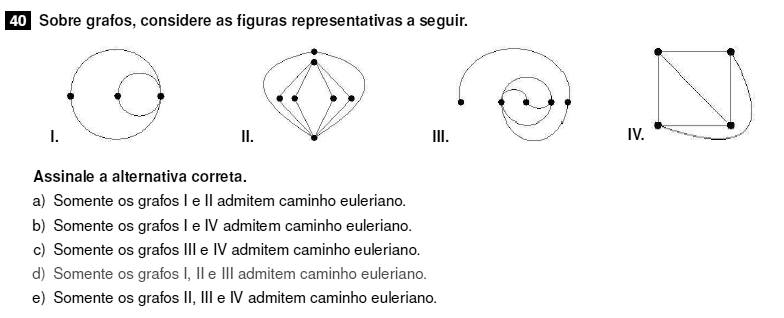
Um grafo $G$ é dito Euleriano se há uma trilha fechada (que não repete vértices) que contém cada uma das arestas de $G$.

I) Correto. Não repete vértices em pelo menos uma trilha fechada (ciclo).

II) Correto. Idem acima.

III) Correto. Idem acima.

IV) Incorreto. Não há trilha fechada possível.

Resposta : d

a) Incorreta. Por definição a cadeia vazia não altera o estado do autômato, ou seja, se começou em $\alpha$ o próximo estado também é $\alpha$, quando a entrada é vazia.

b) Incorreta. Não foi dito se o autômato é determinístico ou não, portanto, pode ficar em laço infinito.

c) Incorreta. Essa condição não define um autômato finito determinístico. Estes são determinados pelo fato de um símbolo de entrada determinar apenas um estado possível subsequente.

d) Correta. Conforme explicado no item a.

e) Incorreta. Um autômato finito não determinístico tem um ou mais opções de escolha para cada símbolo de entrada. Nada foi dito a esse respeito.

Resposta: d

[Em dúvida sobre a conta]
$2GHz=2\cdot10^9/s$. Em cinco segundos: $5\cdot 2\cdot 10^{9}=10^{10}$ ciclos para executar $P$ em $C_1$. No computador $C_2$ temos $0,5\cdot10^{10}=5\cdot10^9/s=5GHz$.

Resposta: c

a) Incorreta. Sempre que há acesso à recursos compartilhados temos condições de corrida, com múltiplos processadores ou não.

b) Incorreta. Há vários mecanismos que podem ser utilizados para controle de acesso simultâneo, não somente semáforos.

c) Correto. O BCP pode suspender interrupções à CPU enquanto trata o processo ativo para evitar problemas de acesso simultâneo.

d) Incorreto. Deve-se sempre organizar o acesso à recursos compartilhados para evitar problemas graves de lógica em operações diversas.

e) Incorreto. Idem acima.

Resposta: c

Ainda não respondida.

A ordem de acesso, do mais rápido para o mais lento, ou seja, a hierarquia de memórias em um computador, é: Registradores, Cache L1, Cache L2, Memória Ram e disco rígido.

Resposta: e

Ainda não respondida.

Ainda não respondida.

Ainda não respondida.

Ainda não respondida.

Ainda não respondida.

a) Incorreta. Não busca fazendo o join, na mesma tabela, para obter registros com crm diferente.

b) Correta. Faz o join com a própria tabela checando os nomes iguais e crms diferentes.

c) Incorreta. Vai acontecer um erro porque o atalho M2 não existe.

d) Incorreta. Natural Join é um comando que não existe.

e) Incorreta. Não é possível executar um from desta forma.

Resposta : b

I) Incorreta. Os requisitos podem ser produzidos ao longo das sprints, que são agendas curtas de desenvolvimento focado de parte de um projeto.

II) Correta. O desenvolvimento incremental entrega mais valor aos interessados do que todo o projeto de uma vez, além de facilitar o acompanhamento do que está sendo produzido.

III) Correta. Conforme explicado acima, nas entregas parciais os interessados podem avaliar o que já foi feito e discutir pendências e outras necessidades.

IV) Correta. Idem itens acima.

Resposta: e

I) Correta. Operações de escrita precisam travar o recurso para poder efetivar a mudança e para termos um conflito, os pedidos devem ser emitidos por transações distintas.

II) Correta. O ARIES é um algoritmo de recuperação utilizado em grandes SGBDs.

III) Incorreta. O bloqueio compartilhado permite que operações de leitura sejam efetuadas em um mesmo item por duas transações distintas.

IV) Incorreta. ACID vem de: Atomicidade, Consistência, Isolamento, Durabilidade.

Resposta: a

I) Correta. No teste caixa preta não há acesso ao código fonte, mas somente às chamadas disponíveis e seus resultados. O testador interage com o sistema e reporta problemas encontrados nas funcionalidades.

II) Correto. No teste caixa branca o código é avaliada para garantir que a execução de certas operações resulta nos valores esperados, ou seja, que estruturas de controle, laços, etc. produzem o efeito desejado.

III) Incorreta. Estruturas de controle servem para ramificar um programa em diferentes caminhos, dependendo de um teste lógico.

IV) Incorreta. Teste baseados em cenários se concentram em funcionalidades que o usuário pode executar no sistema.

Resposta: a

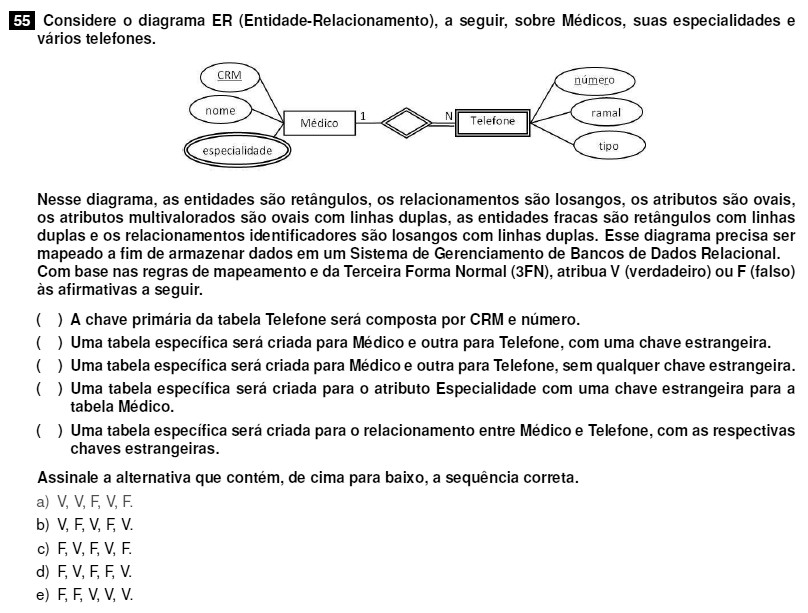
V) Um mesmo CRM não pode estar ligado ao mesmo telefone duas vezes.

V) Os dados de telefone só dependem da chave telefone e não das propriedades de médico, logo, devem ficar em outra tabela.

F) Se não houver chave estrangeira não conseguimos relacionar de forma consistência as informações de ambas as tabelas.

V) Como especialidade não depende da chave primária de médico, deve ficar em outra tabela e ligada via chave estrangeira.

F) Se a tabela de telefone tem o CRM do médico, então não precisamos de uma nova tabela para relacionar os dados.

Resposta: a

I) Correta. O algoritmo de Gouraud é um técnica de interpolação utilizada para produzir sombreamento contínuo em superfícies que são representadas por malhas poligonais. A suavidade será tão melhor quanto a resolução de cada malha.

II) Correta. Na projeção paralela, objeto tem forma e tamanho como se fossem reais e para exibí-lo devemos transformar os pontos no plano de visualização, que é retangular.

III) Correta. O algoritmo de linha de Bresenham visa aproximar uma linha reta entre dois pontos para desenho de imagens através de pixeis como uma matriz.

IV) Incorreta. O efeito de serrilhado acontece quando utilizamos pixeis em subamostragem para desenhar uma imagem.

Resposta : d

Os filtros lineares tem a grande desvantagem de afetar áreas sem ruído de uma imagem. Em contrapartida, os filtros não lineares, como modo e mediana, definem algoritmos de como certas máscaras podem ser aplicadas. No caso do Moda, ele utiliza o nível digital de um vizinho frequente para determinar o valor do elemento analisado. Isso é feito por um histograma e toma-se o valor central dos dados. Caso ele não seja encontrado, é tomado o valor modal mais próximo ao central. O filtro de Mediana utiliza a mediana dos níveis digitais dos vizinhos. Ordenam-se os valores e escolhe-se o dado que divide o conjunto em duas partes iguais.

Logo, devemos escolher o filtro de mediana para remover o ruído da imagem.

Resposta: b

I) Técnica de Phong é um tipo de interpolação utilizada para iluminação e sombreamento. Letra C.

II) É uma técnica de ordenação de objetos que serão renderizados para pintura em ordem decrescente, do mais afastado para o mais próximo. Elementos ao fundo vão ficar escondidos por aqueles que estiverem sobrepostos com ordenamento mais baixo. Letra A.

III) O algoritmo Cohen-Sutherland serve para remover linhas que estão fora de uma determinada área de interesse. Letra B.

IV) BSP (Binary Space Partitioning) é um método para particionar o espaço de modo que recursivamente subdivide um espaço euclidiano em dois conjuntos convexos através de partições hiperplanas. Esse processo gera formas em estruturas de dado de árvore ou árvores BSP. Letra D.

V) Bézier é um tipo de aproximação de curvas por pontos de controle. Letra E.

Resposta: d

I) Incorreta. A geração de um histograma da imagem revela a distribuição da intensidade ou das cores de seus pixeis. A comparação não revela que são impressões visuais de uma mesma cena.

II) Correta. As imagens são as mesmas, mas com a equalização aplicada à imagem C com base no histograma de B, ou seja, uma melhoria nas intensidades dos níveis de cinza.

III) Correta. O histograma é um gráfico em 2D que exibe as intensidades de cores ou contraste e brilho médio de uma imagem.

IV) Correta. É possível avaliar os níveis de contrante e brilho com base no histograma (gráfico deslocado).

Resposta: e

A técnica mipmap é uma forma de aplicar filtros, de maneira eficiente, à textura, em cada polígono, para melhorar a qualidade da imagem. Uma imagem grande que ocupa um espaço menor do que o seu tamanho na tela não precisa ser processada inteiramente. A textura fica 33% maior, que implica em pouco overhead de memória.

Resposta: b

I) Incorreta. A diferença principal entre mono e multimodo é que a primeira possui um núcleo mais largo (entre 62,5 e 50 micrômetros, no mono, de 8 até 10 micrômetros), fazendo com que a luz se propague de maneira dispersa, com menores velocidades. A atenuação é um fenômeno que diminui a potência do sinal propagando e é mais pronunciado no multimodo do que no monomodo.

II) Incorreta. A largura de banda se refere a frequência (Hz) na transmissão de informações.

III) Correta. Fibras ópticas utilizam sinal luminoso para propagação de informação.

IV) Correta. Alguns cabos coaxiais podem chegar até 10Ghz de frequência de transmissão.

Resposta: c

a) Incorreta. O sistema gerenciador de uma máquina virtual pode ser instalado em diferentes tipos de hardware, não havendo esse tipo de restrição.

b) Correta. Enquanto há recursos disponíveis, várias máquinas virtuais podem ser executadas no mesmo computador.

c) Incorreta. Uma máquina virtual pode ser executada em modo isolado de outros programas, não tendo acesso à recursos compartilhados e outras estruturas.

d) Incorreta. Podemos rodar uma máquina virtual Linux em Windows e vice-versa.

e) Incorreta. A máquina virtual pode consumir bastante CPU e memória de uma máquina física, mas no geral isso pode ser configurado e gerenciado.

Resposta: b

a) Incorreta. O IPSec tem o seu cabeçalho de autenticação e de empacotamento.

b) Incorreta. Seu uso é opcional no IPv4.

c) Incorreta. Pode-se implementar uma conexão em túnel tipo VPN usando IPSec.

d) Correta. O SA é uma relação entre uma ou mais partes para descrever como as entidades vão usar serviços seguros que se comunicam.

e) Incorreta. O protocolo tem o modo de autenticação em seus cabeçalhos para proteção dos dados.

Resposta: d

a) Incorreta. O relógio de Lamport lida com sincronia temporal (ordem de eventos) em sistemas distribuídos.

b) Incorreta. O controle central não necessariamente coordenada as operações entre os processos.

c) Incorreta. O algoritmo de Maekawa serve para tratar problemas de exclusão mútua em sistemas distribuídos.

d) Incorreta. Se a mensagem de quem é o líder não circular por todos os sites do anel, então a eleição da liderança não funciona.

e) Correta. O algoritmo de Bully utiliza um identificar numérico, de prioridade no sistema, para efetuar a eleição do coordenador. Funciona em diferentes topologias.

Resposta: e

V) Correta.

V) Correta.

F) Incorreta. Funciona na camada de aplicação pelo UDP (User Datagram Protocol).

V) DNS (Domain Name Server) é um serviço de pesquisa e conversão de nomes de domínio para o IP do servidor registrado e deve ser distribuído para evitar falhas nas pesquisas.

F) Não existe esse método no protocolo HTTP.

Resposta: a

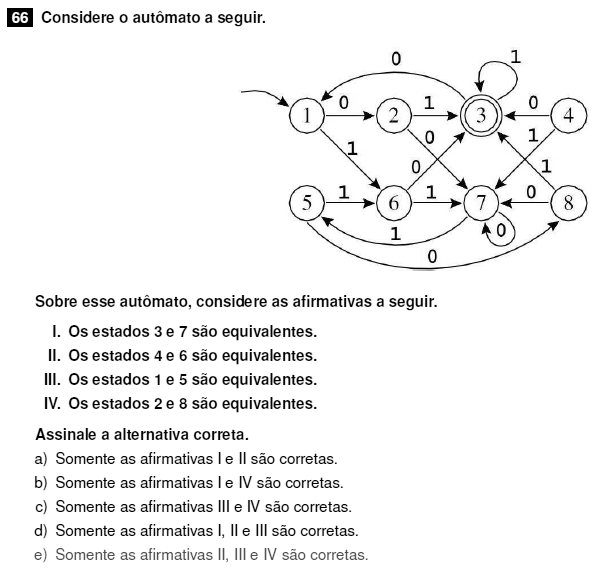
I) Incorreta. O estado 7 é modificado em loop quando recebe o símbolo 0, enquanto no 3 é o símbolo 1.

II) Correta. Aceitam ou rejeitam a mesma palavra.

III) Correta. Aceitam ou rejeitam a mesma palavra.

IV) Correta. Aceitam ou rejeitam a mesma palavra.

Resposta : e

Resposta : c

Ainda não respondida.

I) Correta. A técnica Hill Climbling usa análise numérica para uma busca local, que vai refinando por mudanças incrementais até uma solução aceitável.

II) Correta. A técnica Best first utiliza uma regra para abrir e explorar os nós, podendo ser através de uma função heurística.

III) Correta.

IV) Incorreta. A busca é apenas local, procurando e refinando soluções.

Resposta: d

Ainda não respondida.