Quando falamos de linguagens de programação podemos dividí-las em dois grandes grupos, conforme vimos na seção anterior:

1. Aquelas cujo o significado associado não é importante;
2. Aquelas que tem uma interpretação com significado.

A sintaxe é a área da linguística que cuida da verificação gramatical de programas, sendo que a semântica, por outro lado, busca dar interpretação aos símbolos. A sintaxe não deve se importar com a semântica, em princípio, mas somente com a validade da linguagem utilizada dentro de um certo alfabeto e suas regras. Uma outra parte das estruturas de linguagem é o léxico, um tipo especial de análise sintática, onde se avalia o conjunto de palavras disponíveis formadas a partir do alfabeto.

Há três formalismo utilizados para abordar o problema de avaliação de linguagens:

1. Operacional → Também chamado de reconhecedor, análise uma entrada para determinar sua validade para mudar um estado do sistema;
2. Axiomático → Refere-se às regras dos componentes da linguagem;
3. Denotacional → Também chamado de funcional, analisa as regras de formação das palavras admissíveis da linguagem.

Se $\Sigma$ representa um alfabeto, $\Sigma^*$ representa todas as palavras possíveis e $\Sigma^+=\Sigma^*-\{\epsilon\}$, onde $\epsilon$ é o elemento neutro (ou vazio). Uma linguagem formal, ou linguagem, é qualquer subconjunto L de $\Sigma^*$. O conjunto das partes do conjunto de palavras possível é dado por $2^{\Sigma^*}$.

Uma linguagem de programação é definida pelo conjunto de todos os programas (palavras) da linguagem.

Uma gramática é um conjunto finito de regras que, quando aplicadas em sequência, geram palavras. Uma gramática de Chomsky, gramática irrestrita ou apenas gramática é uma quádrupla ordenada $G=(V,T,P,S)$ onde

V = conjunto de símbolos variáveis ou não terminais
T = conjunto de símbolos terminais disjuntos de V

P = (V $\cup$ T)+ → (V $\cup$ T)* : é uma relação finita, dita relação de produções ou simplesmente produções. cada par é chamado de regra de produção ou apenas produção.

S = elemento distinto de V ou símbolo inicial ou variável inicial.

Regras de produção: definem as condições de geração das palavras em uma dada linguagem, ou seja, o processo de derivação com base na gramática.

Relação de derivação: par da relação de derivação, dada por $\Rightarrow$, com mesmo domínio e codomínio de P, onde um par $\langle \alpha, \beta \rangle$ representa a relação, ou na forma infixada $\alpha \Rightarrow \beta$. Uma derivação é uma substituição de uma subpalavra de acordo com uma regra de produção.

Seja L uma linguagem gerada pela gramática G, escrevemos L(G) , L=GERA(G), ou, por ex:

$L(G)=\{w\in T^*\;|\;S\Rightarrow ^+w\}$

onde $\Rightarrow^+$ exclui o carácter vazio.

São equivalentes duas gramáticas $G_1$ e $G_2$ se e somente se $L(G_1)=L'(G_2)$.

Gramáticas regulares podem ser restritas em suas regras de produção por algumas formas. Uma delas é através de gramáticas lineares (à direita, à esquerda, unitária à direita, unitária à esquerda). Uma gramática é dita regular se é uma gramática linear. Gramáticas regulares podem ser construídas a partir de autômatos finitos determinísticos.

As linguagens são organizadas em hierarquias, pensadas assim originalmente pelo linguista Noam Chomsky.

Linguagens livres de contexto são muito importantes na hierarquia e divididas em: regulares e de programação.

Linguagens regulares são uma classe de linguagens ditas mais simples, ou seja, podemos desenvolver algoritmos de reconhecimento (geração ou conversão) onde o formalismo é baixa complexidade, permite grande eficiência e implementação mais prática.

O lema do bombeamento, também conhecido como lema do bombeamento para linguagens regulares, é um importante teorema da teoria das linguagens formais e autômatos. Ele descreve uma propriedade fundamental das linguagens regulares e fornece um critério para provar que determinada linguagem não é regular.

O lema do bombeamento foi introduzido por Y. Bar-Hillel, Micha Perles e Eli Shamir. Eles estabeleceram o lema do bombeamento como uma ferramenta teórica para demonstrar a não regularidade de certas linguagens.

A ideia central do lema do bombeamento é que se uma linguagem é regular, então qualquer palavra suficientemente longa pertencente a essa linguagem pode ser dividida em partes que podem removidas ou repetidas um número arbitrário de vezes, mantendo-se dentro da linguagem. Em outras palavras, se uma palavra longa faz parte de uma linguagem regular, podemos "bombeá-la" (repetir uma parte dela) e ainda assim obter palavras válidas da linguagem.

Esta é uma ferramenta poderosa na teoria das linguagens formais, pois permite provar a não regularidade de uma linguagem de maneira relativamente simples. Ele é frequentemente usado para mostrar que certas linguagens não podem ser reconhecidas por autômatos finitos determinísticos (AFDs) ou autômatos finitos não determinísticos (AFNs), que são modelos computacionais para as linguagens regulares.

A importância do lema do bombeamento reside na sua utilidade para identificar linguagens não regulares. Ele nos fornece um critério para provar que determinada linguagem não é regular, o que é essencial para a compreensão das classes de linguagens formais. Além disso, o lema do bombeamento desempenha um papel central na teoria da computabilidade e na análise de complexidade de algoritmos.

No entanto, é importante destacar que o lema do bombeamento não é uma ferramenta geral para provar que uma linguagem é regular. Ele apenas fornece um critério para provar que uma linguagem não é regular. Existem linguagens que não satisfazem as condições do lema do bombeamento e ainda assim não são regulares.

Linguagens de programação implementam regras (em alguns casos) estritas sobre balanceamento de limitadores (parênteses, chaves, colchetes, etc…). Seus algoritmos de implementação também são simples e normalmente eficientes. Outros exemplos de aplicação de linguagens livre de contexto são: analisadores sintáticos, tradutores e processadores de texto.

Para estudá-las utilizamos os formalismos de gramática livre de contexto e autômatos com pilhas. Além disso, os seguintes tópicos são importantes no estudo dessas linguagens:

• Árvores de derivação: Permite analisar a derivação de uma palavra onde o primeiro elemento está na raiz e o terminado em uma das folhas;
• Gramática ambígua: Estuda o comportamento quando duas ou mais árvores representam a mesma palavra;
• Simplificação de gramática: Torna mais simples um sistema de produção sem reduzir o poder gerador da gramática;
• Forma normal: Adiciona restrições rígidas sem reduzir o poder gerador da gramática.

As linguagens livres de contexto são definidas a partir das gramáticas livres de contexto, que são quádruplas $G=(V,T,P,S)$, cuja regra de produção $P$ é dada por $A\rightarrow \alpha$ onde A é uma variável de V e $\alpha$ uma palavra de $(V\cup T)^*$, isso quer dizer, é uma gramática onde cada produção contém exatamente uma variável, ou de outra forma, a variável A deriva $\alpha$ sem precisar analisar os símbolos anteriores ou posteriores (contexto). Logo, se G é uma gramática livre de contexto então, a linguagem gerada por G é do contexto se

$$ GERA(G)=\{ w\in T^* \; |\; S\Rightarrow^+w \} $$

Toda linguagem regular pode ser descrita por uma expressão chamada de regular, ou expressão regular, que é um tipo de formalismo denotacional ou gerador, onde inferimos a construção das palavras da linguagem alvo. Definidas as seguintes expressões como regulares $\emptyset, \{ \epsilon \}, \{x\}$ , por indução provamos que quando r e s são expressões regulares pela linguagens R e S:

1. união: (r+s) é uma expressão regular e denota $R\cup S$
2. concatenação: (rs) é uma expressão regular e denota $R\;S=\{ uv | u\in R \; e\; v\in S \}$
3. concatenação sucessiva: $(r^*)$ é expressão regular e denota $R^*$

Uma linguagem é regular se, e somente se, é possível construir um autômato finito (determinístico ou não) que reconheça essa linguagem.

Um reconhecedor é um tipo de máquina abstrata simples que analisa se uma dada entrada é reconhecida ou não (aceita / rejeita). Os principais tipos são:

1. Autômato finito
2. Autômato com pilha
3. Máquina de Turing

Linguagens livres do contexto são fechadas sobre união, concatenação e fecho estrela (*), mas não pra intersecção e complementação.

Kleene star é dada por:

$$ L^*=\cup_{n\geq0}L^n $$

Operações úteis:

1. Construir novas linguagens regulares a partir das existentes (define-se uma álgebra);
2. Provas propriedades;
3. Construir algoritmos.

Para definir se uma linguagem é regular, podemos representá-la por um dos formalismos apresentados (autômato finito, expressão regular ou gramática regular). Para saber se ela não é, pode se utilizar o lema do bombeamento (explicado nos parágrafos a seguir) para provar por absurdo.

O lema do bombeamento lida com ciclos de transição quando a palavra de entrada tem mais símbolos do que estados possíveis no autômato, mas isso não quer dizer que a palavra é rejeitada.

Seja G uma quádrupla para uma gramática livre do contexto. Existe um algoritmo para decidir se $L(G)$ é vazia ou não e infinita ou não. Para isso deve-se escrever o autômato finito M e avaliar cada um dos casos com base no tamanho da entrada e o número de estados de M.

Também é uma propriedade importante definir quando duas linguagens regulares são iguais. Isso é feito através de um algoritmo simples, por um teorema, e a comparação das linguagens geradas por autômatos finitos.

É importante saber que formalismos utilizados nas linguagens regulares podem ser traduzidos entre si. Por exemplo, autômatos finitos determinísticos para expressões regulares ou gramáticas regulares, ou ainda para autômatos finitos não determinísticos e vice-versa.

Sempre que usamos autômatos finitos, qualquer solução obtida é ótima, exceto por eventual redundância de estados. As redundâncias de estados podem ser eliminadas pelo processo de minimização de um autômato finito, ou seja, gerar um novo autômato equivalente mas com menor número de estados. Dois autômatos tem estados equivalentes quando aceitam/rejeitam uma mesma palavra w.

Algoritmos de reconhecimento para linguagens livre de contexto:

1. Autômato com pilha descendente;
2. Algoritmo de Cocke-Younger-Kasami;
3. Algoritmo de Early.

Eles são classificados como top-down (ou preditivo) e bottom-up. O primeiro constrói uma árvore de derivação para a palavra de entrada pela raiz, com direção dos ramos às folhas. No último, a árvore vai no sentido contrário, em direção à raiz.

Um sistema de estados finitos é uma abordagem matemática, um modelo abstrato, para descrever como entrada e saída são interpretadas de forma discreta, ou seja, esse sistema pode somente assumir um número finito e predefinido de estados, onde um estado deve se basear somente nas informações anteriores para definir o próximo. É possível descrever mecanicamente todos os estados possível do sistema, sendo no entanto, inviável em cenários mais complexos como memória de computador ou cérebro humano. No primeiro caso porque o modelo assume memória infinita na teoria da computabilidade e o segundo porque há cerca de $2^{35}$ células, o que torna o processo combinatório ineficiente em termos práticos.

Ao construirmos um sistema podemos utilizar três abordagens distintas para descrever sua composição, ou seja, como montar esquemas mais complexos de outros mais simples:

• Sequencial: O próximo componente é executado assim que o atual é finalizado;
• Concorrente: Componente independentes que executam estados sem ordem definida, ao mesmo tempo;
• Não determinista: O próximo componente tem opções de execução o que faz com que entradas iguais não gerem o mesmo resultado sempre. Pode ser interno (sistema define o próximo estado de forma aleatória) ou externo (a escolha é definida fora do sistema).

Autômatos são sistemas de estados finitos que utilizam o modelo sequencial para modelar seus componentes. É muito útil para estudos teóricos em computação como compiladores, semântica formal e modelos para concorrência. São divididos em:

1. Determinístico: o sistema lê o símbolo de entrada e só pode selecionar um estado subsequente;
2. Não-determinístico: Há opções de escolha, onde o sistema deve executar algum processo para definir a seleção do próximo estado;
3. Movimentos vazios: Sistema pode mudar de estado sem ler um símbolo associado.

É possível provar que os três tipos acima tem poder computacional equivalente.

O autômato finito determinístico (AFD) é composto de três partes:

• Fita: Entrada finita que contém o símbolo a ser lido;
• Unidade de controle: Informa o estado atual do sistema e lê a fita se movendo sempre em um sentido (definido como direita);
• Programa: Regra de transição após leitura do símbolo.

A fita não pode ser regravada (conteúdo não pode ser alterado), os símbolos ocupam toda a fita e pertencem ao alfabeto de entrada do sistema. A unidade de controle, ou controle finito, deve ler uma célula de cada vez e chamar o programa para determinar o próximo estado do autômato.

Um AFD pode ser definido por uma 5-upla ordenada $M=(\Sigma,Q, \delta, q_0,F)$ onde

1. $\Sigma$ : Alfabeto de símbolos de entrada;
2. $Q$ : Conjunto de estados possíveis (finito);
3. $\delta$ : Programa utiliza nas transições de estado: $\delta \;: \;Q \times \Sigma \rightarrow Q$ ou $\sigma(p,a)=q$ , onde p é o estado atual e a um símbolo, gerando o novo estado q;
4. $q_0$ : Estado inicial. $q_0\in Q$.
5. $F$ : Subconjunto de Q que representa os estados finais.

Autômatos podem ser representados por gráficos onde

• Estados são nós, representados por círculos;
• Transições são arestas entre nós, com a marcação do símbolo utilizado;
• Estados iniciais e finais devem ser marcados como tais;
• Transições paralelas devem ser informadas com os símbolos necessários ou a regra.

Também podemos representar os AFDs por matrizes.

Como um AFD não tem memória, uma palavra w deve ser quebrada em símbolos e o programa chamado repetidas vezes para cada símbolo até a condição de parada ser detectada. Sempre deve existir uma parada porque a entrada é finita.

Qualquer AFD pode ser visto como um grafo finito direto.

São dois casos onde o AFD assume a parada de processamento:

1. Após aceitar o último símbolo, vai para estado final: ACEITA;
2. Após o último símbolo, vai para estado não final ou entra em estado indefinido para o parâmetro: REJEITA.

A função programa estendida é utilizada para descrever as sucessivas aplicações de uma função $\delta$ aos símbolos da palavra de entrada e serve para definir a linguagem aceita ou rejeitada pelo AFD.

Os autômatos finitos não-determinísticos (AFN) são importantes no tratamento de problemas de concorrência e na teoria de computação, além de linguagens formais. Qualquer AFN pode ser simulado por um AFD. O programa, neste caso, poderá escolher aleatoriamente o próximo estado com base nas opções, isso é feito de forma paralela, sendo que cada caminho não influi no estado, fita ou unidade de controle, ou seja, cada alternativa é investigada simultaneamente. Um AFN é definido como uma 5-upla ordenada $M=(\Sigma, Q, \delta, q_0, F)$ onde o que muda do caso AFD é a função programa $\delta$, que agora escrevemos

$$ \delta=Q\times \Sigma \rightarrow 2^Q $$

ou $\delta(p,a)=\{ q_1,q_2,...,q_n \}$. Se $\delta(p,a)=\emptyset$ então o AFN para e rejeita a entrada.

Qualquer AFD com movimentos vazios pode ser representado por um AFN.

As linguagens livres de contexto podem ser associadas ao formalismo de autômatos com pilha, que é uma modificação do autômato finito, adicionando-lhe memória auxiliar. O armazenamento pode ser tão grande quanto se queira e esse modelo é útil para resolver problemas que não eram possíveis com AFD ou AFN. Qualquer linguagem livre de contexto pode ser reconhecida por um autômato com pilha, sendo a estrutura de memória suficiente para organizar os estados. A pilha começa inicialmente vazia (exceto pelo símbolo inicial de marcação) e o autômato para quando for aceito um estado final. Semelhante ao AFD, há quatro partes no autômato de pilha:

1. Fita
2. Pilha
3. Unidade de controle: agora com cabeça de fita e de pilha
4. Programa: Lê a fita e pode gravar na fita o estado da máquina.

A pilha segue a estrutura de dados de mesmo nome, sendo que o elemento no topo é o primeiro a ser removido e é removido após esse passo.

Esse formalismo ainda pode ser modificado para aceitar múltiplas pilhas. No caso de um autômato com duas pilhas, temos um poder computacional similar à máquina de Turing, que é o dispositivo mais geral de computação. Se um problema é solucionado por um autômato com mais de duas pilhas, então é solucionado por um com duas pilhas.

Em 1936, Alan Turing desenvolveu um formalismo abstrato para uma máquina computacional universal, que hoje é o modelo mais utilizado em teoria da computação. Uma máquina de Turing é um autômato com uma fita de tamanho indefinido (quão grande quanto se queira) e que pode ser usada como entrada, saída e memória auxiliar.

As linguagens aceitas por máquinas de Turing são ditas recursivamente enumeráveis, ou de tipo 0 segundo a hierarquia de Chomsky, ou seja, representam a classe mais geral de linguagens que podem ser reconhecidas por um sistema mecânica em tempo finito. A gramática utilizada para representá-las é chamada de irrestrita, ou seja, não possui restrições em suas produções, de forma que a gramática tem o mesmo poder computacional do que a máquina de Turing, no formalismo.

Há casos onde, dada uma palavra w, a máquina de Turing não vai terminar o processamento, ficará indefinidamente executando a função. Podemos encontrar um subconjunto de linguagens enumeráveis recursivas que podem ser executadas por uma máquina de Turing. Os problemas desse tipo são ditos solucionáveis.

As linguagens do tipo 1 ou sensíveis ao contexto, podem ser aceitar por uma máquina de Turing com fita limitada, isto é, a fita tem um tamanho máximo. O formalismo utilizado na descrição é a gramática sensível ao contexto.

Na fita, os seguintes são os símbolos válidos:

1. Pertence ao alfabeto de entrada;
2. Pertence ao alfabeto auxiliar;
3. Ser “branco”;
4. Ser “marcador de início de fita”.

A unidade de controle pode se mover para direita ou esquerda na fita, ler e gravar um símbolo, sendo que esses movimentos são determinados pelo programa.

Definição: Uma máquina de Turing (MT) é uma 8-upla $M=(\Sigma,Q,\delta,q_0,F,V,\beta,\star)$, onde

• $\Sigma$ : alfabeto de símbolos de entrada;
• Q : conjunto de estados possíveis;
• $\delta$ : função programa. $\delta :Q\times (\Sigma \cup V\cup \{\beta, \star\})\rightarrow Q \times (\Sigma\cup V\cup\{\beta,\star\})\times \{E,D\}$, onde E e D são esquerda e direita respectivamente, ou, de forma resumida: $\delta (p,x)=(q,y,m)$ , onde q é o novo estado, y o símbolo gravado e m o sentido do movimento.
• $q_0$ : estado inicial
• F : subconjunto de Q, ou estados finais.
• V : alfabeto auxiliar (pode ser vazio)
• $\beta$ : símbolo especial branco
• $\star$ : símbolo de início ou marcador de fita.

A máquina vai executar sucessivamente a função programa até incorrer em uma parada. Como dito anteriormente, há a possibilidade de loops infinitos.

Uma linguagem L dita recursiva é tal que existe ao menos uma máquina de Turing que Aceita(M) = L, ou Rejeita(M) = ~L, onde ~L é o complemento de L.

Há modelos equivalentes à maquina de Turing, de mesmo poder computacional, como:

1. Autômato com múltiplas pilhas;
2. Máquina de Turing não determinística;
3. Máquina de Turing com fita infinita à esquerda e à direita;
4. Máquina de Turing com múltiplas fitas;
5. Máquina de Turing multidimensional;
6. Máquina de Turing com múltiplas cabeças;
7. Combinações de modificações sobre a máquina de Turing.

É composta das linguagens regulares ou tipo 3, livres de contexto ou tipo 2, sensíveis ao contexto ou tipo 1 e recursivamente enumeráveis ou tipo 0.

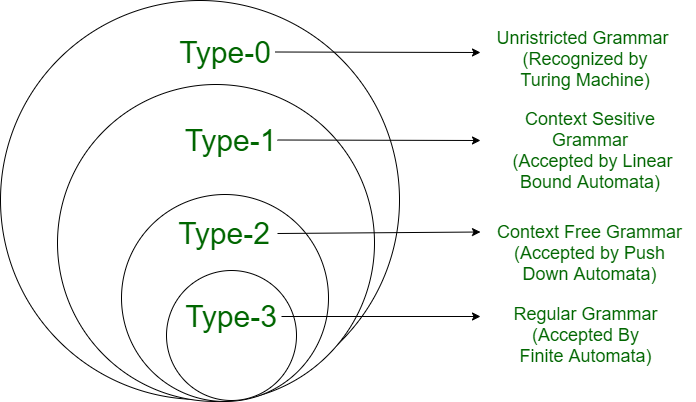
De acordo com a tese de Church-Turing, sobre a natureza de funções computáveis, que declara que uma função nos números naturais pode ser calculada por algum meio efetivo se, e somente se, pode ser executada em uma máquina de Turing. Um meio efetivo pode ser descrito como o uso de papel e lápis para resolver o problema (método mecânico, procedural e com número finito de instruções).

Uma função recursiva parcial é tal que pode ser “computada”. É definida como: $f$ é uma função de um subconjunto $S$ de $X$ para $Y pode ser calculada através de uma máquina de Turing.

A tese de Church-Turing, formulada na década de 1930 por Alonzo Church e Alan Turing, é um princípio fundamental na ciência da computação que diz respeito à natureza dos problemas que podem ser resolvidos (ou "decididos") por computadores. Embora não seja uma teoria formalmente provada, a tese tem sido amplamente aceita e utilizada como um guia na pesquisa de computação e matemática.

Contexto Histórico

No início do século 20, matemáticos e lógicos começaram a explorar os limites do que poderia ser computado. Questões sobre decidibilidade, ou seja, se certos problemas matemáticos podem ter uma solução definitiva encontrada por meio de um procedimento algorítmico, tornaram-se centrais. Em 1931, Kurt Gödel publicou seus teoremas de incompletude, mostrando que existem afirmações verdadeiras em sistemas formais que não podem ser provadas dentro desses sistemas. Isso lançou dúvidas sobre a capacidade de resolver todos os problemas matemáticos por meio de métodos computacionais. Todo esse desenvolvimento surgiu dos 23 problemas de Hilbert, propostos em 1900. O décimo problema questionava se existia um procedimento algorítmico para determinar a solubilidade de equações diofantinas arbitrárias. Uma equação diofantina é uma equação polinomial com coeficientes inteiros para a qual se busca soluções inteiras. A questão de Hilbert, portanto, indagava sobre a possibilidade de decidir, de forma geral e sistemática, se dadas equações desse tipo têm solução inteira.

Tentativas Iniciais

Inicialmente, as tentativas de resolver o décimo problema de Hilbert concentraram-se em desenvolver métodos específicos para classes particulares de equações diofantinas. Ao longo das primeiras décadas do século XX, diversos matemáticos contribuíram com avanços significativos para o estudo de equações diofantinas, embora um método geral e abrangente para todas as equações parecesse cada vez mais inatingível.

Contribuições de Church e Turing

• Alonzo Church: Em 1936, Church introduziu o conceito de funções recursivas e o cálculo lambda, uma forma de representar algoritmos e funções computáveis. Ele propôs que as funções efetivamente calculáveis são precisamente aquelas que podem ser definidas no cálculo lambda, formulando a noção de "decidibilidade" em termos de computabilidade.

• Alan Turing: No mesmo ano, Turing introduziu o conceito de uma máquina abstrata, agora conhecida como Máquina de Turing, capaz de simular qualquer processo de cálculo algorítmico. Ele argumentou que esta máquina poderia modelar o processo de cálculo humano, seguindo um conjunto de instruções simples. Turing usou sua máquina para resolver o "Entscheidungsproblem" (problema de decisão) proposto por David Hilbert, mostrando que não existe um algoritmo geral que possa decidir a verdade ou falsidade de todas as afirmações matemáticas. Esse resultado destacou limitações fundamentais na decidibilidade matemática.

Tese de Church-Turing

A tese de Church-Turing é uma hipótese sobre a natureza da computabilidade mecânica. Ela postula que uma função sobre os números naturais pode ser calculada por um algoritmo se, e somente se, ela pode ser computada por uma Máquina de Turing. Em outras palavras, ela estabelece que o conceito de "computável" é equivalente a ser calculável por esses meios teóricos. Essa tese não foi originalmente formulada como um teorema a ser provado, mas sim como uma noção intuitiva baseada nas observações de Church e Turing sobre a natureza do cálculo algorítmico.

Impacto na Decidibilidade

A tese de Church-Turing tem implicações profundas para a teoria da decidibilidade. Ela fornece uma base para entender quais problemas são computacionalmente solúveis e quais permanecem indecidíveis. Por exemplo, o problema da parada, que pergunta se uma dada máquina de Turing vai parar ou continuar a rodar indefinidamente para uma entrada específica, é um problema clássico que foi provado ser indecidível por Turing. Isso significa que não existe um algoritmo geral que possa determinar, para qualquer máquina de Turing e entrada, se a máquina eventualmente para ou não.

Na teoria da computação, um dos tópicos mais fascinantes é o estudo de problemas indecidíveis - questões para as quais não existe um algoritmo que possa fornecer uma resposta correta para todas as possíveis entradas. Este campo explora os limites do que pode ser resolvido por máquinas e algoritmos, lançando luz sobre a natureza fundamental da computação.

Linguagens Decidíveis

Uma linguagem é um conjunto de strings sobre um alfabeto. Uma linguagem é dita decidível (ou recursivamente enumerável) se existe uma máquina de Turing que pode aceitar todas as strings na linguagem e rejeitar todas as strings que não pertencem à linguagem. Essencialmente, para qualquer entrada, a máquina de Turing irá parar em um estado de aceitação ou rejeição após um número finito de etapas. Exemplos de linguagens decidíveis incluem a linguagem de todas as strings binárias ou a linguagem de todas as strings que representam números primos.

O Problema da Parada e o Método de Diagonalização

O problema da parada é um dos problemas mais famosos em teoria da computação e foi introduzido por Alan Turing em 1936. Este problema pergunta se é possível criar um algoritmo que, dado como entrada qualquer programa de computador e uma entrada para esse programa, determinará corretamente se o programa para ou continua a executar indefinidamente para essa entrada. Turing provou que tal algoritmo não pode existir, utilizando um argumento conhecido como método de diagonalização. Este método envolve a criação de uma tabela imaginária onde as linhas representam programas e as colunas representam entradas possíveis. Ao tentar construir um programa que decida o problema da parada, chegamos a uma contradição, pois tal programa teria que ser capaz de decidir sua própria parada, o que é impossível.

Linguagem Turing-irreconhecível

Uma linguagem é dita Turing-irreconhecível se não existe uma máquina de Turing que possa reconhecer as strings na linguagem. Para tais linguagens, não apenas não podemos decidir se uma string específica pertence à linguagem, como também não podemos construir uma máquina de Turing que liste todas as strings que pertencem à linguagem (ou seja, não são recursivamente enumeráveis). Um exemplo de uma linguagem Turing-irreconhecível é o complemento do problema da parada, que consiste em todas as strings que não descrevem máquinas de Turing que param em uma determinada entrada. Esse resultado mostra os limites inerentes do que nossos algoritmos podem alcançar, independentemente de quão poderosos ou sofisticados eles sejam.

Estudar problemas indecidíveis nos ajuda a entender os limites fundamentais da computação, mostrando que existem perguntas que estão além do alcance de qualquer máquina de calcular, não importa quão avançada ela seja. Esses conceitos não apenas fundamentam a ciência da computação teórica mas também influenciam a forma como abordamos problemas práticos em áreas como verificação de software, inteligência artificial e além, reforçando a importância de reconhecer as fronteiras do que é computacionalmente possível.

Primeiro teorema: Nenhum sistema consistente de axiomas, onde os teoremas podem passar por um procedimento de listagem (um algoritmo por exemplo), pode provar todas as proposições verdadeiras sobre a aritmética. Corolário: Sempre há afirmações verdadeiras, mas que não podem ser provadas.

Segundo Teorema: Uma teoria, dita recursivamente enumerável e que pode provar certas proposições aritméticas básicas, além de enunciados da teoria da prova, só pode provar sua consistência se, e somente se, for inconsistente.

Quando falamos sobre complexidade de algoritmos introduzimos algumas notações importantes para avaliar como o tempo varia com o tamanho da entrada. Vimos exemplos de casos onde a performance lenta estava associada com complexidades quadráticas ($n^2$) ou exponenciais ($x^k)$, com $x$ um número inteiro positivo. Podemos olhar uma classe de problemas mais geral, ou seja, queremos definir e avaliar o que é um algoritmo rápido e o que são problemas tratáveis em computação.

Temos três classes básicas de problemas computacionais:

1. Otimização: Lida com casos que pedem máximo ou mínimo de algum objeto;
2. Busca: Queremos encontrar um objeto com determinadas propriedades em alguma estrutura;
3. Decisão: Informa se proposição admite resposta do tipo “sim” ou “não”.

Há ligações entre os três problemas, isto é, podemos converter a resposta de uma classe para outra. Em um caso ideal, o algoritmo criado deve informar se o problema é intratável ou retornar sua solução, mas na maioria das vezes este não é caso. Muitos problemas não são possíveis nem mesmo de saber se tem uma solução.

Dizemos que um algoritmo resolve um problema de modo polinomial avaliando a sua complexidade no pior caso, ou seja, ele é limitado por cima por uma função do tipo polinomial. Esses são razoavelmente rápidos, em comparação com exponenciais por exemplo $2^n$. Caso o problema não tenha um algoritmo dito polinomial, o chamamos de “não-polinomial”, isto é, ainda não temos um algoritmo polinomal para tratá-lo no momento, mas isso pode mudar no futuro. Chamamos de classe P todos os problemas que podem ser resolvidos em tempo polinomial $t(n)$.

Podemos definir que um dado problema é fácil se pudermos verificar sua solução, mesmo sem ter um algoritmo de solução formal. Por exemplo, encontrar a solução de uma equação de segunda grau é trivial. Um problema de decisão é dito razoável se há uma forma de verificar que tem solução em tempo polinomial. A classe NP (non-deterministic polynomial) lida com o conjunto de problemas que não são vericáveis em tempo polinomial.

A questão P=NP ou P≠NP analisa se P é apenas uma parte de NP (subconjunto) ou se eles são iguais, mas ainda não sabemos disso. A questão fica então da seguinte forma: "Será que todo problema com solução que pode ser verificada por um algoritmo polinomal também pode ser resolvido por um algoritmo polinomial?".

Ao analisar a classe NP podemos separar os problemas em “mais fáceis” e “mais difíceis”. Isso é o mesmo que dizer que existe um problema geral X e um subproblema Y, tal que Y pode ser reduzido a uma instância de X. Se X está na classe P então Y também está. X é dito NP-difícil se para qualquer problema x da classe NP, x é polinomialmente redutível. Um problema é dito NP-completo se for ao mesmo tempo NP-difícil e estiver em NP. Em resumo:

$P\neq NP, iif P\cap NPC =\emptyset$

O artigo seminal de Stephen Cook, intitulado "The Complexity of Theorem-Proving Procedures" (A Complexidade dos Procedimentos de Prova de Teoremas), foi apresentado no Terceiro Simpósio Anual da ACM sobre Teoria da Computação em 1971. Este trabalho inovador introduziu o conceito de NP-completude, estabelecendo a estrutura fundamental para o campo da complexidade computacional.

No seu artigo, Cook definiu uma classe de problemas conhecidos como "NP-completos", que são problemas em NP que são pelo menos tão difíceis quanto qualquer outro problema em NP. Ele introduziu a noção de que se qualquer problema NP-completo pudesse ser resolvido em tempo polinomial, então todos os problemas em NP também poderiam ser resolvidos em tempo polinomial, mostrando efetivamente que P = NP. Este conceito se baseia na ideia de que os problemas NP-completos são uma espécie de "pedra angular" na compreensão da estrutura de NP.

A principal contribuição do artigo de Cook foi a identificação do primeiro problema que ele provou ser NP-completo: o problema da satisfabilidade booleana (SAT). SAT pergunta se uma fórmula booleana dada pode ser tornada verdadeira atribuindo valores verdadeiros às suas variáveis. Cook mostrou que SAT é NP-completo ao demonstrar uma redução em tempo polinomial de qualquer problema em NP para SAT. Isso significa que resolver SAT em tempo polinomial implica que todos os problemas em NP também podem ser resolvidos em tempo polinomial.

A importância do artigo de Cook não pode ser superestimada. Foi o primeiro a articular formalmente o problema P vs. NP e a identificar um exemplo concreto de um problema NP-completo. O trabalho de Cook abriu a porta para uma compreensão mais ampla da complexidade computacional e influenciou diretamente o desenvolvimento do campo. Após seu artigo, a identificação e o estudo de problemas NP-completos se tornaram um foco central da ciência da computação, levando à descoberta de muitos outros problemas NP-completos em vários domínios.

O artigo de Cook não apenas introduziu uma nova maneira de pensar sobre problemas computacionais, mas também preparou o terreno para pesquisas subsequentes na área. O conceito de NP-completude desde então se tornou uma ferramenta fundamental para entender a dificuldade dos problemas computacionais e para classificá-los com base em suas complexidades computacionais inerentes.

As contribuições de Stephen Cook foram reconhecidas com o Prêmio Turing em 1982, uma das maiores honrarias em ciência da computação, por seu trabalho sobre a teoria da complexidade computacional e, em particular, por seu artigo sobre a complexidade dos procedimentos de prova de teoremas.

Na teoria da computação, a redutibilidade é um conceito chave que permite comparar a complexidade de diferentes problemas, estabelecendo uma forma de "traduzir" um problema em outro. Essencialmente, se um problema A pode ser reduzido a um problema B, qualquer solução para B pode ser usada para resolver A, implicando que A não é mais difícil de resolver do que B. Este conceito é crucial para entender as relações entre diferentes classes de problemas e para identificar problemas intrinsecamente difíceis. Vamos explorar dois métodos importantes de redutibilidade: redução via histórias de computação e redutibilidade por mapeamento.

Teoria das Linguagens e Redução via Histórias de Computação

A teoria das linguagens na computação lida com o estudo de linguagens formais e suas propriedades computacionais. Dentro deste contexto, a redução via histórias de computação é uma técnica que permite reduzir um problema de decisão (determinar se uma entrada pertence a uma linguagem específica) a outro, utilizando a "história" de uma computação como ponte entre eles. Uma história de computação é essencialmente um registro dos estados por que uma máquina de Turing passa ao processar uma entrada.

Por exemplo, se queremos provar que um problema A é NP-completo, podemos tentar reduzi-lo a um problema B já conhecido por ser NP-completo, mostrando que qualquer instância de A pode ser transformada em uma instância de B de forma que a solução de B nos dê a solução para A. Para fazer isso, podemos construir uma máquina de Turing que simula a execução de A, e usar a história dessa computação para criar uma instância de B. Essa abordagem é particularmente útil para provar a NP-completude de problemas, demonstrando que eles são, pelo menos, tão difíceis quanto os problemas mais difíceis em NP.

Redutibilidade por Mapeamento

A redutibilidade por mapeamento é outra técnica fundamental na teoria da computação, que envolve a construção de uma função computável (ou mapeamento) que transforma instâncias de um problema A em instâncias de um problema B de tal forma que a resposta para a instância transformada de B corresponda diretamente à resposta da instância original de A. Este tipo de redutibilidade é especialmente importante para o estudo da complexidade computacional, pois permite classificar problemas com base em sua dificuldade relativa.

A redutibilidade por mapeamento é comumente usada para demonstrar que certos problemas são indecidíveis, mostrando que se pudéssemos resolver um determinado problema (como o problema da parada), então seríamos capazes de resolver outro problema que já sabemos ser indecidível. Da mesma forma, é uma ferramenta essencial para estabelecer a NP-completude, onde uma função de redução por mapeamento transforma instâncias de um problema conhecido por ser NP-completo em instâncias do problema em questão, demonstrando assim que este último é pelo menos tão difícil quanto o primeiro.

Ambas as formas de redutibilidade, via histórias de computação e por mapeamento, são pilares fundamentais na análise da complexidade dos problemas na teoria da computação. Elas não apenas ajudam a classificar problemas em termos de sua dificuldade computacional mas também oferecem insights sobre a natureza da computabilidade e os limites do que pode ser alcançado através de algoritmos.

Referências:

1. Linguagens Formais e autômatos - Paulo Blauth Menezes
2. Problemas NP-Completo
3. Propriedades das Linguagens Livres do Contexto
4. General Recursive Function
5. Undecidable problems

< 12 - Linguagens de Programação > 14 - Organização de Arquivos e Dados