Algoritmos são receitas passo-a-passo para se resolver um problema finito em tempo finito. Devem ser escrito de forma a não conter ambiguidades em suas ramificações, de forma que o computador não conseguiria definir um caminho para solucionar uma problema sem direcionamento claro e objetivo. Algoritmos devem ter ao menos três qualidades:

1. Cada passo deve ser uma instrução possível de ser realizada;
2. A ordem dos passos deve ser precisa;
3. Deve ter um fim.

Algoritmos podem ter uma estrutura sequencial ou paralela, podem ter condições (grupo de ações com base em condição) e repetições (sequência de comandos executado enquanto uma condição é verdade).

Os algoritmos sequenciais são aqueles em que as instruções são executadas uma após a outra, em ordem específica, seguindo uma sequência lógica. Cada instrução só é executada após a conclusão da anterior. Por exemplo, se temos um algoritmo para somar dois números, a instrução de leitura dos números deve ocorrer antes da instrução de soma.

Por outro lado, os algoritmos paralelos envolvem a execução simultânea de várias instruções. Essa abordagem é comumente usada em computação paralela e distribuída, onde diferentes partes do algoritmo podem ser executadas em paralelo em vários processadores ou sistemas.

Para começar o desenvolvimento de um algoritmo podemos iniciar com uma proposição genérica e ir incrementando os passos com as estruturas básicas. De forma simples, definimos os dados de entrada, o processamento e a saída.

Existem várias formas de representar algoritmos, sendo duas das mais comuns a representação textual e a representação gráfica. Na representação textual, os algoritmos são descritos por meio de uma linguagem de programação ou uma linguagem próxima à linguagem natural. Já na representação gráfica, os algoritmos são representados por meio de diagramas, como fluxogramas, que mostram visualmente o fluxo de execução das instruções.

Um algoritmo pode ser representado por pseudocódigo ou português estruturado. O pseudocódigo é uma técnica de representar o algoritmo como se fosse uma linguagem de programação, com condicionais, laços e variáveis, facilitando o entendimento do problema. Ele é baseado no PDL (Program Design Language), que é uma representação de linguagem.

A complexidade dos algoritmos refere-se à quantidade de recursos, como tempo e espaço, necessários para executá-lo. A análise da complexidade é importante para avaliar o desempenho e a eficiência de um algoritmo. Algoritmos mais eficientes consomem menos recursos e executam mais rapidamente.

Qualquer computador comum utiliza como base o conjunto binário {0,1}, ou seja, toda e qualquer instrução ou valor deve ser representado como sequências de 0 ou 1. O bit é a unidade que representa ou 0 ou 1, nunca ambos. O byte é uma sequência de 8 bits e tem $2^{8}$ valores possíveis (0 ou 1 em cada uma das 8 posições). Cada bloco de bytes pode valer um número natural, um inteiro ou um caráctere. Normalmente se trabalha com valores que estão entre 0 e $2^{64}$-1. Para escrevermos os números inteiros, definimos o tamanho da sequência de bytes, por exemplo, 32, e teremos um intervalo dado por

$$ -2^{32-1}...2^{32-1}-1 $$

Onde usamos a estrutura de 8s bits, com s variando entre 1,2,4 e 8, ou seja, se s=4, então

$2^{8s}=2^{32}$, de modo que podemos definir e escrever os intervalos.

Para saber se o número é positivo ou negativo, usamos a notação complemento-de-dois (two’s complement) onde se o primeiro bit for 0, o valor é positivo, caso contrário, negativo.

0000 = +0
0111 = +7
1000 = -8
1110 = -2

Para representarmos caracteres utilizamos a tabela ASCII, onde cada símbolo é definido por 1 byte, podendo representar até 128 elementos.

Há ainda 33 caracteres de controle, como \0, \t, \,n.

Como tipos básicos, na linguagem C por exemplo, temos o int e o char, que representam inteiros ou caracteres, respectivamente. Inteiros e caracteres podem ter sinal ou não, e, caso não tenham, utilizamos a palavra-reservada unsigned int / char. Quando precisamos de números maiores com precisão de ponto flutuante, utilizamos short ou long.

Quando representamos números em uma cadeia de bytes utilizamos a operação de módulo para conseguir um valor fora do intervalo. E como fazemos para representar uma sequência de caracteres? Utilizamos um vetor de bytes, que é sequência de bytes ordenada, onde cada byte é um char e o último byte é o nulo 00000000. Chamamos a cadeia de bytes de caracteres de string.

Quando queremos empacotar tipos diferentes em uma mesma estrutura, por exemplo, int e char, podemos usar um objeto chamado struct, na linguagem C. Eles funcionam como se fossem um novo tipo de dados, onde o objeto tem como primeiro endereço a primeira variável e seu fim na última. Se criarmos um struct como abaixo

    
        struct placaCarro{
            char[4] texto;
            int numero;
        }
    

usamos 4 bytes para o texto (1 byte para cada letra) e 4 bytes para o número, formando uma sequência em memória de 8 bytes.

A principal diferença entre os tipos de dados básicos e estruturados em C é que os tipos básicos representam valores individuais, enquanto os tipos estruturados representam conjuntos de valores relacionados. Os tipos básicos são usados para armazenar dados simples, enquanto os tipos estruturados são usados para representar entidades mais complexas e organizadas.

Além disso, os tipos estruturados podem ser combinados e aninhados, permitindo a criação de estruturas mais complexas e hierárquicas. Essa flexibilidade é especialmente útil quando você precisa lidar com dados mais complexos, como registros, listas encadeadas ou árvores.

    
        struct Pessoa {
            char nome[50];
            int idade;
            float altura;
        };
    

No exemplo acima, a estrutura "Pessoa" possui três membros: nome, idade e altura. O membro "nome" é do tipo char (array de caracteres), o membro "idade" é do tipo int e o membro "altura" é do tipo float. Essa estrutura permite que você armazene informações relacionadas a uma pessoa em um único objeto, facilitando o acesso e manipulação desses dados.

Em quase todas as linguagens de programação temos comandos que são recorrentes. O mais natural deles é o de declarar tipos de variáveis, seu identificador e o valor inicial. Em C, quando queremos declarar um inteiro, usamos:

    
        int valor = 1;
    

Sendo que esse padrão é simples e claro. Em outras linguagens, que o tipo não é exigido, como JavaScript, utilizamos:

    
        nome = "João";
    

Podemos executar e compor operações aritméticas (+,-,*,/,%) e lógicas (&&, ||, ^^, !) com as variáveis, além de relacioná-las segundo símbolos como >, <, ≥, ≤, == e ! ==.

Quando queremos avaliar uma condição utilizamos palavras reservadas em estruturas condicionais (if, elseif, switch, etc…) ou laços quando queremos repetir um trecho de código (for, while, do).

Programas recursivos lidam com chamadas ao mesmo código com instâncias menores do problema inicial, sendo que quando o caso base é encontrado há retorno da função e então as várias chamadas vão sendo reduzidas até a primeira, de maneira que o problema tem ou não uma solução.

Algoritmos recursivos podem causar problemas de performance não somente por causa da complexidade de tempo, mas também de espaço. Cada chamada da função ocupa o espaço das variáveis de escopo novamente e isso será multiplicado pelo número de vezes que a recursão é feita. Um exemplo de recursão em C está abaixo:

#include 
#include 
#include 
#define MAX 50
#define printlinha() { printf("\n"); }
int encontrarMaximo(int vetor[], int posicao, int maximoAtual)
{
    if(posicao >= MAX)
    return maximoAtual;
    if(vetor[posicao] > maximoAtual)
    maximoAtual = vetor[posicao];
    return encontrarMaximo(vetor, posicao+1, maximoAtual);
}
int main()
{
    int vetor[MAX];

    for(int i = 0; i < MAX; i++)
    {
        vetor[i] = rand () % 100;
        printf("%d", vetor[i]);
        printlinha();
    }

    printf("O max encontrado foi: %d", encontrarMaximo(vetor, 0, 0));
    free(vetor);

    return EXIT_SUCCESS;
}

                

Propriedades dos Algoritmos Recursivos:

• Caso base: algoritmos recursivos dependem de um caso base ou condição de término que significa quando a recursão deve parar. O caso base garante que o algoritmo eventualmente atinja uma condição de término, evitando a recursão infinita.
• Passo Recursivo: Algoritmos recursivos decompõem um problema em subproblemas menores da mesma natureza. O algoritmo chama a si mesmo (recursão) para resolver cada subproblema até atingir o caso base.
• Dividir e conquistar: algoritmos recursivos geralmente seguem uma estratégia de "dividir e conquistar". Eles dividem um problema em subproblemas menores e independentes, resolvem cada subproblema independentemente (via recursão) e, em seguida, combinam os resultados para obter a solução final.

Problemas com algoritmos recursivos:

• Stack Overflow: Se um algoritmo recursivo não tiver um caso base adequado ou se as chamadas recursivas não forem estruturadas adequadamente, isso pode levar ao estouro da pilha. Isso ocorre quando a pilha de chamadas, que armazena informações sobre chamadas de funções ativas, se esgota, resultando em um erro de tempo de execução.
• Cálculos duplicados: algoritmos recursivos podem encontrar cálculos duplicados ao resolver subproblemas. Se o mesmo subproblema for encontrado várias vezes, cálculos redundantes podem ocorrer, afetando o desempenho. Técnicas como memoização (resultados intermediários de armazenamento em cache) podem atenuar esse problema.
• Considerações de Complexidade:
  A complexidade de um algoritmo recursivo pode ser analisada usando os conceitos de complexidade de tempo e complexidade de espaço.
• Complexidade de tempo: A complexidade de tempo de um algoritmo recursivo depende do número de vezes que o algoritmo faz chamadas recursivas e do custo computacional de cada chamada. Relações de recorrência e análise matemática são comumente usadas para determinar a complexidade de tempo de algoritmos recursivos.
• Complexidade espacial: algoritmos recursivos utilizam a pilha de chamadas para gerenciar chamadas de função e armazenar resultados intermediários. A complexidade do espaço é determinada pela profundidade máxima da recursão, que corresponde ao número máximo de chamadas de função ativas na pilha de chamadas.

Abaixo temos outro exemplo clássico, do algoritmo recursivo de fibonacci, em Python:

def fibonacci(n):
if n <= 1:
    return n
else:
    return fibonacci(n-1) + fibonacci(n-2)

# Example usage:
print(fibonacci(6))  # Output: 8

Calcular o tempo exato de execução de um algoritmo recursivo usando matemática pode ser um desafio devido à complexidade das chamadas de função recursivas e possíveis variações com base em valores de entrada específicos. No entanto, você pode estimar o tempo de execução analisando o número de chamadas recursivas e o trabalho executado em cada nível. Aqui está uma abordagem geral para estimar o tempo de execução de um algoritmo recursivo:

• Identifique a relação de recorrência: determine a relação matemática entre o tamanho da entrada e o número de chamadas recursivas feitas pelo algoritmo. Essa relação de recorrência descreve como o tamanho do problema diminui a cada chamada recursiva.
• Resolva a relação de recorrência: analise a relação de recorrência para encontrar uma solução de forma fechada ou um limite superior para o número de chamadas recursivas. Essa solução normalmente será expressa em função do tamanho da entrada ou da profundidade da recursão.
• Analise o trabalho realizado em cada nível: determine a quantidade de trabalho realizado em cada nível de recursão. Isso pode envolver a contagem do número de operações aritméticas, comparações ou outros cálculos relevantes. Se o trabalho realizado variar com base no problema ou na entrada, talvez seja necessário considerar o cenário de pior caso ou de caso médio.
• Combine a análise: multiplique o número de chamadas recursivas em cada nível pelo trabalho realizado naquele nível. Some esses valores para todos os níveis de recursão para estimar o trabalho total executado pelo algoritmo.
• Considere a complexidade: converta a análise de trabalho em uma estimativa de complexidade de tempo, como a notação Big O, para capturar a taxa de crescimento do algoritmo à medida que o tamanho da entrada aumenta. Esta etapa permite expressar o tempo de execução em função do tamanho da entrada, em vez de um valor de tempo específico.

Na medida que aumentamos o tamanho de um programa, passando de poucas funções para dezenas, centenas e até milhares ou milhões, devemos nos preocupar com a organização dos arquivos e da estrutura de código. Alguns conceitos são importantes para ajudar nessa empreitada. Quando separamos, por exemplo, em linguagem C, o arquivo de header .h da implementação .c, estamos abstraindo o código com a lógica de uma função para uma linha apenas, uma assinatura que indica os parâmetros de entrada e o tipo de saída daquela função. O mesmo ocorre em linguagens orientadas à objetos, como C# e Java, onde podemos criar interfaces que são contratos de como as classes precisam descrever certos métodos, sem especificar seu conteúdo, mas sim a parte que é exposta publicamente. Abstração então, é um modo de realçar as características essenciais de um problema, omitindo detalhes que não são relevantes, sem que o entendimento geral seja perdido.

Na medida que separamos o sistema em partes com responsabilidade limitadas e poucas dependências de outros elementos, criamos módulos, que são subprogramas que se comunicam e provem mais organização e manutenibilidade no longo prazo. Esse problema começa a ficar importante não somente quando há mais código a ser desenvolvido e o ambiente é complexo, mas também porque na medida que mais desenvolvedores se juntam à equipe, a separação de quem faz o quê fica mais clara, evitando conflitos entre códigos diferentes no mesmo bloco do programa. Além disso, fica mais fácil de criar e executar testes unitários e de integração, contribuindo para a depuração de partes importantes do sistema.

Um projeto de software finalizado nunca está livre de bugs. Terminar, nesse caso, é sinônimo de entregar o produto em um ambiente produtivo, onde os clientes interessados podem acessá-lo e utilizá-lo sem restrições. Entretanto, quando um problema é encontrado, que não tinha sido previsto no tempo de desenvolvimento, o que os desenvolvedores fazem? O processo básico para descobrir o que aconteceu é chamado de depuração (debug). Depurar é analisar de forma rigorosa um ou mais processos para entender com profundidade o motivo do sistema se comportar de maneira imprevista, utilizando como insumos o que os usuários reportaram. Normalmente as informações reportadas pelo usuário são confusas, imprecisas e sem detalhes, então, a equipe precisa aprender a fazer boas perguntas para começar a investigação do problema. O passo primordial para o sucesso da depuração é tentar reproduzir o bug, ou seja, simular as mesmas condições que o usuário enfrentou e receber a mesma resposta. Com isso a avaliação do erro no código fica bem mais fácil. Entretanto, nem sempre a vida é tão fácil assim. Pode-se passar horas e horas tentando entender o que aconteceu e, sem detalhes mais relevantes do caso, pode ser muito difícil avaliar o comportamento do sistema. Nesse sentido, equipes modernas e bem organizadas definem processos de avaliação de qualidade (QA), tentando identificar e arrumar problemas no software antes de liberá-lo ao ambiente produtivo. Reunir evidências com detalhes e criar formulários com boas perguntas também são importantes para facilitar o trabalho de identificação e correção de bugs, além de organizar treinamentos e cursos para aprendizado contínuo dos desenvolvedores.

Resumo:

• Faça boas perguntas e reúna evidências sobre o problema;
• Implemente bons logs de depuração em pontos críticos do software;
• Disponibilize mensagens de erro com significado para a equipe de manutenção;
• Exercite periodicamente a equipe com problemas de depuração;
• Tente replicar o problema!
Crie uma área de QA com processos rígidos e documente tudo.

Imagine uma sequência de caracteres qualquer, ou seja, um elemento em seguida do outro, sem qualquer ordenação específica, apenas uma lista de um determinado alfabeto (conjunto origem dos caracteres). Chamamos essa sequência de cadeia de caracteres (string).

Quando queremos encontrar um determinado padrão, estamos casando um subconjunto dessa cadeia, e as vezes queremos achar a primeira ou um certo número de ocorrências desse padrão. Isso é aplicado em diversas áreas, desde edição de textos, recuperação de informação e estudo do DNA.

Notação utilizada:

Alfabeto: $\Sigma=\{a,b,...z,0,1,2,...,9\}$, de tamanho c;

Texto: É um arranjo $T[1...n]$ de tamanho n;

Padrão: Arranjo de tamanho m≤n , $P[1...m]$

Queremos então saber as ocorrências de P em T, onde normalmente n>>m (n muito maior do que m).

Temos duas categorias de algoritmos: quando conhecemos P e T de antemão (pré-processados) e quando não o conhecemos e devemos processá-los em tempo real. Isso muda as complexidades de tempo e espaço. No último caso: $O(mn)$ de tempo e $O(1)$ de espaço. Para o caso pré-processado: $O(n)$ para tempo e $O(m+c)$ para espaço.

No caso de um algoritmo com dados pré-processados podemos construir um índice de dados, que vai facilitar a pesquisa futura. Com isso a complexidade se reduz para $O(log\;n)$ e a de espaço para $O(n)$. Na medida que aumentamos o índice a complexidade de espaço aumenta, mas isso seria compensado pela rapidez na pesquisa dos dados. Índices mais conhecidos:

1. Arquivos invertidos;
2. Árvores trie e de Patricia;
3. Arranjos de sufixos.

O tipo arquivo invertido armazena as ocorrências de determinados termos no texto, como uma lista de frequências para estatística. A regra de crescimento do vocabulário é dada pela Lei de Heaps: Um texto contendo n palavras tem tamanho $V=Kn^\beta=O(n^\beta)$, com os parâmetros K e $\beta$ dependentes do texto, com K no intervalo (10,100) e $\beta\in(0,1)$. Há três fases principais nesse tipo de índice:

1. Pesquisa no vocabulário;
2. Encontrar as ocorrências;
3. Manipular os valores encontrados.

É importante guardar o índice de vocabulário em arquivo separado. Também é importante definir uma ordenação para montar o índice, por exemplo, lexicográfica (order de dicionário). Isso agiliza a busca e reduz o custo de tempo. Um tipo de estrutura de dado comum para arquivo invertido é árvore trie (pronuncia-se “trái”).

O casamento exato de um valor é um pouco mais complexos. Algoritmos:

1. Knuth-Morris-Pratt
2. Shift-And
3. Boyer-Moore-Horspool
4. Boyer-Moore

Por força bruta também podemos identificar o valor procurado, mas o pior caso, quando o padrão não existe no texto, é custoso.

Autômatos e heurísticas podem ser utilizados para resolver o problema da busca em cadeias.

Arquivos de texto podem ser comprimidos para aumentar a velocidade de processamento de símbolos. Algoritmos: Huffman, Ziv-Lempel, Moffat e Katajainen.

O objetivo principal do algoritmo de Huffman é criar uma representação mais eficiente para os dados, atribuindo códigos de tamanho variável a cada símbolo na entrada com base em sua frequência de ocorrência. Os símbolos mais frequentes recebem códigos mais curtos, enquanto os menos frequentes recebem códigos mais longos.

O processo de compressão do algoritmo de Huffman envolve as seguintes etapas:

1. Análise de frequência: O algoritmo examina a entrada e conta a frequência de ocorrência de cada símbolo. Isso pode ser feito por meio de uma tabela de frequência ou uma árvore de frequência.

2. Construção da árvore de Huffman: Com base nas frequências dos símbolos, é construída uma árvore binária chamada árvore de Huffman. Os símbolos são colocados nos nós folha da árvore, enquanto os nós internos representam combinações de símbolos.

3. Atribuição de códigos: Percorrendo a árvore de Huffman, é atribuído um código binário único a cada símbolo. Ao se mover para a esquerda na árvore, o código binário é estendido com um '0', e ao se mover para a direita, é estendido com um '1'. Os códigos atribuídos são prefixos, ou seja, nenhum código é prefixo de outro.

4. Compressão: A entrada original é percorrida novamente, e cada símbolo é substituído pelo seu código correspondente. Essa substituição resulta em uma sequência de bits compactada, que ocupa menos espaço de armazenamento.

5. Descompressão: Para descompactar os dados, é necessário ter acesso à árvore de Huffman original. A sequência compactada é percorrida bit a bit, seguindo os caminhos da árvore de Huffman até que um símbolo seja encontrado. Esse símbolo é então emitido como parte da saída descompactada. O processo continua até que toda a sequência compactada seja processada.

O algoritmo de Huffman é eficiente para dados com distribuição de frequência desigual, pois permite a representação de símbolos mais frequentes com menos bits. No entanto, para dados com distribuição uniforme, onde todos os símbolos têm a mesma frequência, o algoritmo de Huffman não oferece uma vantagem significativa de compressão.

O algoritmo de Lempel-Ziv-Welch (LZW) é um algoritmo de compressão de dados sem perdas amplamente utilizado. Ele foi desenvolvido por Abraham Lempel, Jacob Ziv e Terry Welch no início da década de 1980 e é conhecido por sua eficiência na compactação de dados.

O objetivo do algoritmo LZW é substituir sequências repetitivas de dados por códigos mais curtos, reduzindo assim o tamanho do arquivo comprimido. Ele aproveita a propriedade de que muitos dados contêm padrões repetitivos ou sequências frequentes.

O algoritmo LZW opera por meio de um dicionário que é inicialmente preenchido com uma tabela de símbolos pré-definidos, como caracteres individuais. À medida que a entrada é lida, o algoritmo identifica sequências de símbolos que ainda não estão no dicionário. Essas sequências são adicionadas ao dicionário e substituídas por um código que representa essa sequência.

O processo de compressão do LZW pode ser resumido em etapas:

1. Inicialização do dicionário: O dicionário é preenchido com símbolos pré-definidos, como caracteres únicos.

2. Leitura da entrada: O algoritmo lê a entrada um símbolo de cada vez.

3. Construção de sequências: O algoritmo constrói sequências de símbolos até encontrar uma sequência que não está presente no dicionário.

4. Adição ao dicionário: Quando uma sequência é encontrada pela primeira vez, ela é adicionada ao dicionário, juntamente com um novo código que a representa.

5. Saída dos códigos: À medida que as sequências são encontradas, o código correspondente a cada sequência é emitido como parte da saída comprimida.

6. Atualização do dicionário: O dicionário é continuamente atualizado à medida que novas sequências são encontradas, adicionando-as com seus respectivos códigos.

O algoritmo LZW é conhecido por sua capacidade de criar um dicionário adaptativo durante o processo de compressão, permitindo a codificação de sequências cada vez mais complexas à medida que mais dados são lidos. Isso contribui para a eficiência do algoritmo, especialmente em dados com padrões repetitivos.

Na descompressão, o algoritmo LZW utiliza o mesmo dicionário construído durante a compressão para reconstruir a sequência original de dados. Os códigos da saída comprimida são usados para pesquisar o dicionário e recuperar as sequências correspondentes.

O algoritmo LZW é amplamente utilizado em formatos de compressão de arquivos populares, como GIF, TIFF e PDF. Ele é conhecido por sua eficiência em compressão de texto, imagens e outros tipos de dados com padrões repetitivos.

No entanto, é importante observar que o algoritmo LZW possui algumas limitações. Ele pode apresentar um aumento no tamanho da saída quando aplicado a dados que não contêm padrões repetitivos. Além disso, sua implementação requer um esforço adicional para lidar com questões relacionadas ao tamanho do dicionário e códigos de comprimento variável.

O algoritmo de aproximação de entropia é uma técnica utilizada na ciência da computação para estimar a entropia de uma fonte de dados. A entropia é uma medida da quantidade de informação contida em um conjunto de dados, e a sua estimativa é útil em diversas áreas, como compressão de dados, criptografia e análise de padrões.

O objetivo do algoritmo de aproximação de entropia é calcular uma estimativa razoável da entropia de uma fonte de dados sem a necessidade de analisar todos os seus elementos. Isso é especialmente útil quando lidamos com conjuntos de dados grandes, onde a análise completa pode ser inviável em termos de tempo e recursos computacionais.

O algoritmo de aproximação de entropia é baseado em uma abordagem estatística. Ele utiliza amostragem aleatória dos dados para obter uma visão geral da sua distribuição e, a partir dessa amostra, calcula uma estimativa da entropia.

O processo do algoritmo de aproximação de entropia pode ser resumido em etapas:

1. Seleção da amostra: Uma quantidade representativa de dados é selecionada aleatoriamente do conjunto completo. A seleção da amostra pode ser feita com ou sem substituição, dependendo do método utilizado.

2. Contagem de ocorrências: Na amostra selecionada, as ocorrências de cada elemento são contadas. Isso envolve a criação de um histograma que registra a frequência de cada elemento na amostra.

3. Cálculo da frequência relativa: Com base nas contagens de ocorrências, é calculada a frequência relativa de cada elemento na amostra. A frequência relativa é determinada dividindo o número de ocorrências de um elemento pelo tamanho total da amostra.

4. Cálculo da entropia: Utilizando as frequências relativas, a entropia é estimada por meio de uma fórmula estatística, como a fórmula de Shannon. Essa fórmula leva em consideração a distribuição das frequências relativas para determinar a quantidade de informação contida nos dados.

5. Refinamento da estimativa: Para melhorar a precisão da estimativa, o algoritmo de aproximação de entropia pode repetir as etapas anteriores várias vezes, selecionando diferentes amostras aleatórias e calculando a entropia estimada em cada iteração. A média dessas estimativas pode ser tomada como o valor final da entropia aproximada.

É importante destacar que o algoritmo de aproximação de entropia fornece uma estimativa da entropia e não o valor exato. A precisão da estimativa depende do tamanho e representatividade da amostra selecionada. Quanto maior a amostra, mais precisa será a estimativa.

Uma lista representa muitos elementos do mesmo tipo sequencialmente na memória RAM. Normalmente o vetor que representa a lista começa na posição 0 e vai até n-1, quando há n > 0 elementos na lista.

As listas ordenadas são estruturas de dados lineares em que os elementos são organizados em ordem crescente ou decrescente. Essa ordenação permite uma rápida busca e inserção de elementos. Em C, podemos implementar uma lista ordenada usando um array e garantindo que os elementos sejam inseridos na posição correta.

#define MAX_SIZE 100

int listaOrdenada[MAX_SIZE];
int tamanho = 0;

void inserirListaOrdenada(int valor) {
    int i, j;

    // Encontra a posição correta para inserção
    for (i = 0; i < tamanho; i++) {
        if (listaOrdenada[i] > valor) {
            break;
        }
    }

    // Move os elementos maiores para a direita
    for (j = tamanho; j > i; j--) {
        listaOrdenada[j] = listaOrdenada[j - 1];
    }

    // Insere o valor na posição correta
    listaOrdenada[i] = valor;

    tamanho++;
}

Uma lista encadeada (ou lista ligada) é um tipo de estrutura onde cada elemento tem duas propriedades: seu valor e um ponteiro para o próximo. Para adicionar um novo elemento à lista, basta modificar o ponteiro de próximo do último item, se for adicionado ao final, ou o ponteiro no meio da lista para apontar para o novo item e este para o próximo. Essa operação é de complexidade constante.

    
struct Node {
    int valor;
    struct Node* proximo;
};

struct Node* listaEncadeada = NULL;

void inserirListaEncadeada(int valor) {
    struct Node* novoNode = (struct Node*)malloc(sizeof(struct Node));
    novoNode->valor = valor;
    novoNode->proximo = listaEncadeada;
    listaEncadeada = novoNode;
}
    

A busca de um item pode ser feita com recursão ou de forma iterativa, sendo a recursão mais usada pela clareza e economia de código.

Uma lista ligada circular tem o último item apontando para o primeiro. Em listas duplamente encadeadas, cada item aponta para o anterior e o próximo.

Uma pilha (stack) é um tipo abstrato de dados que armazena elementos empilhando-os, ou seja, ao retirar um item, este será o último adicionado, de forma que o último a ser retirado foi o primeiro a ser inserido. Esse tipo de estrutura é chamado FILO (First-in Last-out). Para adicionar um item usamos o termo “push”, e para remover “pop”.

    
#define MAX_SIZE 100

int pilha[MAX_SIZE];
int topo = -1;

void push(int valor) {
    if (topo < MAX_SIZE - 1) {
        topo++;
        pilha[topo] = valor;
    } else {
        printf("A pilha está cheia!\n");
    }
}

int pop() {
    int valor = -1;
    if (topo >= 0) {
        valor = pilha[topo];
        topo--;
    } else {
        printf("A pilha está vazia!\n");
    }
    return valor;
}

    

Uma filha (queue) é um tipo abstrato de dados que armazena elementos como em uma fila de banco, quem chegar primeiro vai sair primeiro, quem chegar por último sairá por último FIFO (First-in First-out). As operações fundamentais, assim como na pilha, são enfileirar e remover da fila.

    
#define MAX_SIZE 100

int fila[MAX_SIZE];
int frente = -1;
int tras = -1;

void enqueue(int valor) {
    if (tras < MAX_SIZE - 1) {
        if (frente == -1) {
            frente = 0;
        }
        tras++;
        fila[tras] = valor;
    } else {
        printf("A fila está cheia!\n");
    }
}

int dequeue() {
    int valor = -1;
    if (frente != -1 && frente <= tras) {
        valor = fila[frente];
        frente++;
        if (frente > tras) {
            frente = -1;
            tras = -1;
        }
    } else {
        printf("A fila está vazia!\n");
    }
    return valor;
}

    

Antes de falar de árvores precisamos definir uma nova estrutura de dados: Tabela de símbolos (symbol table). Essa ADT tem elementos, do tipo par-valor, e duas operações básicas: “put”, “get”. Não podemos adicionar chaves repetidas na TS. O tempo de busca é proporcional ao número de elementos na tabela.

Uma árvore binária de busca é uma implementação de uma tabela de símbolos onde os elementos estão ordenados, é possível comparar as chaves através de operações elementares. Uma árvore possui nós e folhas (ou galhos), um nó sempre tem ao menos um filho e uma folha não tem filho algum. Em uma árvore binária, o número máximo de filhos de um nó é 2. O nó raiz não tem um pai, ou seja, só tem filhos. Dada um nó qualquer, a sua profundidade é o número de links da raiz até ele. A altura de uma árvore é a profundidade máxima do último nó.

Dizemos que uma árvore é balanceada se a altura estiver perto de $lg(N)$, com $N$ o número de nós.

Para montar uma árvore binária de busca precisamos organizar os elementos com alguma regra de ordenação, por exemplo, os elementos à esquerda do nó pai tem chave menor do que ela e os à direita chaves com valor maior. As operações de inserir e buscar dependem da altura da árvore.

Índices são estruturas que agilizam a busca de informações dentro de uma estrutura de dados. Um exemplo comum é o índice em árvores, como a árvore de busca binária. Essas estruturas de dados organizam os elementos em uma árvore, onde cada nó possui um valor e dois filhos, um à esquerda e outro à direita. A propriedade chave dessas árvores é que todos os valores na subárvore esquerda de um nó são menores do que o valor do próprio nó, enquanto todos os valores na subárvore direita são maiores. Isso permite a busca eficiente, pois podemos descartar metade dos elementos em cada comparação.

Outro exemplo de índice amplamente utilizado é o índice invertido, comumente encontrado em sistemas de busca de texto, como motores de busca na web. Esse tipo de índice mapeia palavras ou termos para as localizações onde essas palavras ocorrem nos documentos. Ele permite uma busca rápida por palavras-chave, identificando rapidamente os documentos relevantes que contêm esses termos.

Um tipo abstrado de dados implementado como árvore é o heap, onde cada nó pai P de um nó filho C respeita uma, e apenas uma, das propriedades:

1. P é maior do que C;
2. P é igual a C;
3. P é menor do que C.

A heap é uma implementação da estrutura abstrata de dados chamada "fila de prioridade", onde o elemento raiz tem a prioridade mais alta (ou mais baixa). É muito útil quando se quer remover o elemento de maior (ou menor) prioridade para processamento.

Existem dois tipos principais de heaps:

• Min-Heap: Em um min-heap, o nó pai tem uma prioridade menor que seus filhos. O elemento com a prioridade mínima reside na raiz do heap.
• Max-Heap: Em um max-heap, o nó pai tem uma prioridade mais alta que seus filhos. O elemento com a prioridade máxima é encontrado na raiz do heap.

Operações comuns de heap:

• Inserção: adicionar um novo elemento ao heap envolve colocá-lo na próxima posição disponível no nível mais inferior e, em seguida, executar uma operação de "heapify" para restaurar a propriedade do heap.
• Exclusão: remover o elemento de prioridade mais alta (ou mais baixa) do heap requer substituí-lo pelo último elemento do heap, seguido por uma operação "heapify" para manter a propriedade do heap.
• Peek: A recuperação do elemento de prioridade mais alta (ou mais baixa) do heap sem removê-lo é realizada acessando a raiz do heap.

Veja um exemplo abaixo de implementação de heap em Python.

import heapq

class MaxHeap:
    def __init__(self):
        self._heap = []

    def is_empty(self):
        return len(self._heap) == 0

    def insert(self, item):
        heapq.heappush(self._heap, -item)  # Multiply by -1 for max-heap

    def delete_max(self):
        if not self.is_empty():
            return -heapq.heappop(self._heap)  # Multiply by -1 for max-heap
        raise IndexError("Heap is empty")

    def peek_max(self):
        if not self.is_empty():
            return -self._heap[0]  # Multiply by -1 for max-heap
        raise IndexError("Heap is empty")

# Example usage:
heap = MaxHeap()
heap.insert(5)
heap.insert(3)
heap.insert(7)

print(heap.peek_max())  # Output: 7

print(heap.delete_max())  # Output: 7
print(heap.delete_max())  # Output: 5

Um método muito útil para reduzir os nós de pesquisa em uma árvore é a poda, ou tree pruning, que remove nós não muito significativos para o problema, resultando em uma árvore mais simples.

A tabela Hash é um tipo de tabela de símbolos em que a chave é dada por um valor gerado por uma função de espalhamento (hash) que não pode se repetir (colisão). O nome espalhamento vem do fato de que os valores estão distribuídos em um intervalo pré-definido. Ela deve ser eficiente na geração dos elementos. Os parâmetros são: M = número de posições na tabela, N número de chaves da tabela de símbolos e $\alpha$=N/M é o fator de carga. O valor do hash está entre 0 e M-1.

Se as chaves estão no domínio dos números, especificamente os inteiros, podemos usar a função modular para gerar o hash.

Uma tabela hash é composta por um array de elementos chamados de "slots" ou "buckets", e cada slot contém uma chave e seu valor correspondente. A principal característica das tabelas hash é o acesso rápido aos dados por meio de uma função de hash.

A função de hash é responsável por converter a chave em um índice no array. Idealmente, essa função deve distribuir as chaves de forma uniforme em todo o espaço de slots disponíveis, minimizando colisões, que ocorrem quando duas chaves são mapeadas para o mesmo índice. No entanto, em alguns casos, colisões são inevitáveis, e diferentes estratégias são usadas para resolvê-las.

Existem várias abordagens para lidar com colisões em tabelas hash. Duas das estratégias mais comuns são:

1. Encadeamento Separado: Nessa estratégia, cada slot contém uma lista encadeada de elementos com chaves diferentes, que são mapeadas para o mesmo índice. Quando ocorre uma colisão, o novo elemento é simplesmente adicionado à lista existente no slot correspondente.

2. Endereçamento Aberto: Nessa estratégia, quando ocorre uma colisão, são explorados outros slots na tabela até encontrar um slot vazio. Existem diferentes técnicas de endereçamento aberto, como sondagem linear, sondagem quadrática e sondagem por duplo hash. Essas técnicas determinam a sequência de slots a serem explorados em caso de colisão.

As tabelas hash têm várias aplicações na ciência da computação. Elas são frequentemente usadas em bancos de dados, sistemas de indexação, caches, compiladores e muitos outros sistemas. Sua eficiência é baseada na capacidade de acesso rápido aos dados, o que permite operações como inserção, recuperação e remoção em tempo constante, em média.

No entanto, é importante considerar alguns aspectos ao usar tabelas hash. O desempenho da tabela hash pode ser afetado pela qualidade da função de hash, pela distribuição das chaves e pela quantidade de colisões. Além disso, o tamanho da tabela precisa ser cuidadosamente escolhido para evitar desperdício de memória ou sobrecarga de colisões.

Diversos algoritmos e estruturas de dados são usados para implementar tabelas hash, como tabelas hash simples, tabelas hash com listas encadeadas, tabelas hash com endereçamento aberto e árvores AVL com tabelas hash, entre outros.

Quando temos uma estrutura de dados preenchida queremos executar operações nela como pesquisa (buscar um item de valor específico) ou ordenação (rearranjar os itens em novas posições). Os algoritmos de busca e ordenação (sorting) resolvem esses problemas. O que deve ser avaliado em cada um dos casos é a complexidade (de tempo e espaço) que depende do tamanho da entrada $n$.

Busca

Um método de busca quer encontrar um elemento que ter determinadas propriedades, inserido em uma estrutura previamente conhecida.

Linear seach: É um tipo de busca em vetores onde se compara elemento a elemento com o valor buscado até o fim da lista. No pior caso é necessário olhar o vetor completo (sem encontrar o valor) e no melhor caso o valor procurado está no primeiro elemento da lista. A complexidade é do tipo $O(n)$ no pior caso.

Binary search: Dado um vetor ordenado de n posições, começamos por olhar para o elemento do meio e verificamos se é maior, igual ou menor que valor procurado. No melhor caso o valor procurado é justamente o elemento central. Caso não seja, olhamos para a metade da lista que contém o intervalo que o valor existe e repetimos o processo até encontrar o valor ou ficarmos com um único item de valor diferente do procurado. A complexidade é de $O(log(n))$, assim como o espaço necessário para executá-lo.

Jump search: Nesse caso pulamos de um elemento $i$ para o próximo $i+k$, ou seja, não é linear, tenta encontrar o valor pulando de item em item por um passo $k$. A complexidade é dada pela quantidade de blocos, ou seja, se a entrada é n, $q=n/k$, em um vetor ordenado, no pior caso teremos $O(q+k-1)$. Para definir o valor ótimo de $k$, usamos:

$$ \frac{d}{dk}(\frac{n}{k}+(k-1))=0\Rightarrow k=\sqrt{n} $$

Interpolation search: Dado um vetor ordenado de n posições, distribuídos de forma uniforme, usamos a seguinte fórmula para pesquisa do valor buscado:

$$ pos=l+\frac{x-a[l]}{a[h]-a[l]}\cdot x(h-l) $$

onde l é o menor índice do array, a[k] o valor do índice na posição k, h é maior índice. No melhor caso o algoritmo tem complexidade constante $O(1)$, apenas uma operação é feita. Se os valores não são distribuídos uniformamente, a busca pode levar mais operações, inclusive com performance pior que o binary search.

Exponential search: Dado um vetor com n posições, verificamos se o valor é igual ao primeiro elemento, caso não seja, montamos uma laço que anda rapidamente pelo vetor (se $i$ é o contador do laço, o próximo passo é dado por $i=i\cdot 2$). A condição deve analisar se $i < n$ e $a[i]≤x$. Caso cheguemos ao fim do vetor, utilizamos a busca binária para pesquisar o elemento na metade final do vetor que ainda não olhamos, por exemplo, $i/2$. A complexidade é dada pela busca binária $O(log(n))$ mais as operações de filtro.

Ordenação (estruturas lineares)

Insertion sort: Tem dois laços: No primeiro, seleciona um elemento do vetor, o remove e usa o segundo para encontrar sua posição, comparando com cada elemento posterior, como num baralho de cartas. Tem complexidade n² e boa performance para vetores pequenos, mas péssima para grandes.

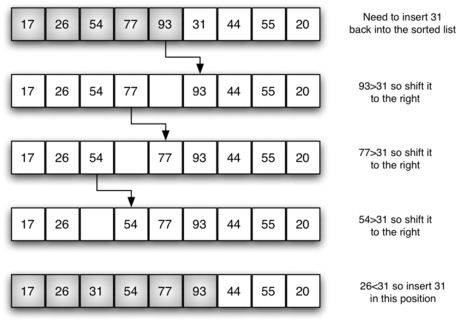
Selection sort: Usa a estratégia de encontrar o menor valor do vetor, mudá-lo de posição, depois o segundo menor e assim por diante, até finalizar a ordenação. Tem performance n², e no pior caso é mais lento que o Insertion Sort.

Bubble sort: Faz múltiplas passagens pelo vetor, comparando e trocando de dois em dois, itens desordenados. Tem complexidade n² e no pior caso fará ao menos uma troca. É normalmente mais ineficiente que os outros métodos.

Shell Sort: Divide a lista original em listas menores comparando pares e trocando suas posições para ordená-los. Para quebrar a lista original em menores utiliza-se o gap, ou intervalo não-contíguo de elementos, ou seja, escolher itens que estão $i$ posições entre si. O algoritmo é finalizado quando o gap é 0 (zero), quando o gap é 1, o método de ordenação é o insertion sort. No pior caso, a complexidade é $O(n^2)$, mas na média, pode ser $O(n^{5/4})$ ou $O(n^{3/2})$.

Merge Sort: Utiliza recursão para dividir a lista original na metade, até que sobre apenas um item em cada ramificação, retornando então depois para combinar os resultados e ordená-los (intercalação). A operações de reduzir a lista à metade tem complexidade $O(log(n))$ e a intercalação ocorre n vezes para cada parte, ou seja, tem-se no final $O(nlog(n))$.

Quick sort: É parecido com merge sort, mas utiliza um valor como pivô da lista, por exemplo, o primeiro elemento. Ele auxilia na divisão da lista, sendo seu ponto de fato na lista final, o ponto de visão, será usado para quebrar a lista para as próximas chamadas. Selecionada a posição do pivô, os elementos serão enviados para o lado correto segundo a ordenação. Para mover o pivô para o ponto correto utilizamos dois marcadores chamados de leftmark e rightmark, com eles vamos comparando elementos leftmark > rightmark e trocando esses itens, até encontrarmos a posição do pivô na lista. Ao final teremos do lado esquerdo elementos menores que o pivô e à direita elementos maiores. Com isso dividimos as duas metades (sem o pivô) e executamos o processo recursivamente nas duas listas até que estejam ordenadas. O algoritmo é $O(nlog(n))$ em geral e necessita de menos espaço que o merge sort, mas no pior caso sua complexidade é $O(n^2)$.

Heap Sort: É um algoritmo de ordenação por seleção muito utilizado em conjuntos com distruição aleatória de dados. A vantagem de performance é que o desempenho em pior caso é parecido com o da média. Pior caso é $O(nlog(n))$ e na média $O(log(n))$. Utiliza uma estrutura de dados tipo heap (que pode ser representada como árvore binária). Depois da organização dos elementos, eles são removidos na ordem desejada.

Os algoritmos de união e busca (também conhecidos como "union-find" ou "disjoint-set") são estruturas de dados que fornecem duas operações fundamentais: "união" e "busca". Esses algoritmos são amplamente utilizados para lidar com o problema de conectividade em conjuntos, especialmente úteis em situações como a determinação de componentes conectados em um grafo, testando a existência de um caminho entre dois nós, e outras aplicações relacionadas a teoria dos grafos e análise de redes.

Problema da Conectividade

O problema da conectividade busca determinar se dois elementos estão no mesmo conjunto ou componente conectado. Por exemplo, em um grafo, o problema seria determinar se existe um caminho entre dois vértices.

União Lenta (Slow Union)

A abordagem mais simples para resolver o problema da conectividade é a união lenta. Nessa abordagem, cada elemento pode ser visto como pertencente a um conjunto, e a operação de união simplesmente mescla dois conjuntos. Isso é feito, por exemplo, atualizando o identificador de conjunto de todos os elementos em um dos conjuntos para ser igual ao do outro conjunto. Embora simples, essa abordagem pode ser ineficiente, pois requer a atualização do identificador de conjunto de potencialmente muitos elementos para cada operação de união, resultando em uma complexidade temporal pior caso de O(n) é o número total de elementos.

União Rápida com Pesos

Para melhorar a eficiência, a união rápida com pesos mantém um peso ou tamanho para cada conjunto. Quando dois conjuntos são unidos, o conjunto menor é anexado ao conjunto maior, garantindo que a árvore resultante seja mais balanceada. Isso reduz a altura máxima da árvore, melhorando o desempenho das operações de busca. A complexidade temporal para cada operação de união ou busca é melhorada para O(log(n)) é o número de elementos.

Compressão de Caminhos Reduzindo pela Metade

A compressão de caminhos é uma técnica de otimização aplicada durante a operação de busca para achatar a estrutura da árvore, fazendo com que todos os nós ao longo do caminho de busca apontem diretamente para a raiz. Uma variante dessa técnica é a compressão de caminhos reduzindo pela metade, onde, durante a busca, cada nó no caminho aponta para seu avô (o nó dois níveis acima), efetivamente reduzindo pela metade o comprimento do caminho. Isso ajuda a acelerar futuras operações de busca e união, aproximando a complexidade temporal de cada operação para O(α(n)) é a inversa da função de Ackermann, uma função que cresce muito lentamente, de tal forma que, para todos os valores práticos de n, pode ser considerada praticamente constante.

Abaixo temos um exemplo de união lenta, em Python:

class SlowUnionFind:
    def __init__(self, size):
        self.root = list(range(size))  # Cada nó é inicialmente sua própria raiz

    def find(self, x):
        return self.root[x]

    def union(self, x, y):
        rootX = self.find(x)
        rootY = self.find(y)
        if rootX != rootY:
            for i in range(len(self.root)):
                if self.root[i] == rootY:
                    self.root[i] = rootX  # Atualiza o identificador do conjunto para unir

    def connected(self, x, y):
        return self.find(x) == self.find(y)

# Exemplo de uso
uf = SlowUnionFind(10)
uf.union(1, 2)
uf.union(2, 3)
print(uf.connected(1, 3))  # Saída: True
print(uf.connected(1, 4))  # Saída: False

Exemplo de união com pesos em Python:

class WeightedQuickUnion:
    def __init__(self, size):
        self.root = list(range(size))
        self.rank = [1] * size  # Mantém o tamanho de cada árvore

    def find(self, x):
        while x != self.root[x]:
            x = self.root[x]
        return x

    def union(self, x, y):
        rootX = self.find(x)
        rootY = self.find(y)
        if rootX != rootY:
            if self.rank[rootX] < self.rank[rootY]:
                self.root[rootX] = rootY
                self.rank[rootY] += self.rank[rootX]
            else:
                self.root[rootY] = rootX
                self.rank[rootX] += self.rank[rootY]

    def connected(self, x, y):
        return self.find(x) == self.find(y)

# Exemplo de uso
uf = WeightedQuickUnion(10)
uf.union(1, 2)
uf.union(2, 3)
print(uf.connected(1, 3))  # Saída: True
print(uf.connected(1, 4))  # Saída: False

Exemplo de compreesão de caminhos em Python:

class CompressedQuickUnion:
    def __init__(self, size):
        self.root = list(range(size))
        self.rank = [1] * size

    def find(self, x):
        if x != self.root[x]:
            self.root[x] = self.find(self.root[x])  # Compressão de caminho
        return self.root[x]

    def union(self, x, y):
        rootX = self.find(x)
        rootY = self.find(y)
        if rootX != rootY:
            if self.rank[rootX] < self.rank[rootY]:
                self.root[rootX] = rootY
            elif self.rank[rootX] > self.rank[rootY]:
                self.root[rootY] = rootX
            else:
                self.root[rootY] = rootX
                self.rank[rootX] += 1

    def connected(self, x, y):
        return self.find(x) == self.find(y)

# Exemplo de uso
uf = CompressedQuickUnion(10)
uf.union(1, 2)
uf.union(2, 3)
print(uf.connected(1, 3))  # Saída: True
print(uf.connected(1, 4))  # Saída: False

São uma classe de algoritmos para identificar objetos em memória que não serão mais utilizados e podem ser limpos da memória (lixo = garbage). A estrutura de pilha (stack) é utilizada normalmente para analisar as referências em memória, tendo como menção o paper “The Tricolor Algorithm” de 1969, que serve de norte para marcar as variáveis com determinadas propriedades quando há menções no código para elas e ir descartando aquelas que não tem referência. Podemos criar um grafo para organizar as referências em memória e avaliar em qualquer momento um determinado critério, como um nó não ter ligação com a raiz. Também é possível rearranjar o grafo para aumentar a performance de busca. No exemplo abaixo, $o_3, o_4$ e $o_5$ não podem mais ser acessados da raiz e devem ser liberados da memória:

A hipóteses generacional análise a frequência do tempo de vida das variáveis, separando-as de acordo com o que já foi visto no sistema, isso provê um filtro para o começo da análise, ao invés de analisar todas as variáveis sempre. As variáveis antigas tem maior probabilidade de serem lixo. Esse processo é utilizado, por exemplo, no JIT (Just in Time) do Java.

Algoritmos de GC tentam otimizar algum padrão do programa para usar a memória com maior eficiência, de forma que é muito difícil criar métricas para compará-los. Algumas métricas importantes são:

1. Minimizar o tempo de uso da memória;
2. Minimizar o tamanho de memória perdido;
3. Minimizar o tamanho de memória necessária para executar a limpeza;
4. Minimizar tempo e recursos necessários do programa para acessar a memória durante sua execução usual;
5. Minimizar o custo de localizar por referência;
6. Minimizar o tempo de queda da aplicação por execução da limpeza;
7. Minimizar a complexidade do algoritmo;
8. Aumentar duração de bateria (se existir);
9. Minimizar o número de escritas em memória flash;

Algoritmos:

Semi-space: É um tipo de algoritmo de cópia, onde cada objeto que pode ser alcançado (reachable) é realocado de um endereço para outro, então, a memória disponível é dividida em duas partes, “from-space” e “to-space”. A limpeza ocorre quando as referências à memória do “to-space” acaba, daí copia-se os objetos do “from-space” para o “to-space”, deixando um espaço livre dos não utilizados. Todas as referências são atualizadas. A vantagem é que os custos de alocação são muito pequenos e a fragmentação é evitada, mas por outro lado, precisa-se de mais memória para funcionar.

Generational GC: A hipóteses generacional analisa a frequência do tempo de vida das variáveis, separando-as de acordo com o que já foi visto no sistema, isso provê um filtro para o começo da limpeza, ao invés de olhar todas as variáveis sempre. As variáveis antigas tem maior probabilidade de serem lixo. Esse processo é utilizado, por exemplo, no JIT (Just in Time) do Java.

Compacting GC: Usa um algoritmo do tipo Mark-Sweep, mas também utiliza um rearranjo dos objetos para evitar fragmentação. Deixa elementos em ordem de alocação, para otimizar a referência.

Incremental GC: Tenta minimizar o tempo de pausa da aplicação durante a limpeza, mas adiciona overhead no processamento do algoritmo. É adequado para aplicações com uso intensivo de gráficos.

Força bruta: busca listar e executar todas as possíveis soluções de um problema, fazendo-o de maneira sistemática. É fácil de implementar, mas normalmente é ineficiente.

    
def maior_numero(lista):
    maior = float('-inf')
    for numero in lista:
        if numero > maior:
            maior = numero
    return maior

    numeros = [4, 2, 9, 1, 7]
    print(maior_numero(numeros))  # Saída: 9
    
    

Pesquisa exaustiva: Gera todas as possíveis soluções de um problema e vai testando cada uma. Problemas: Custo de rota para N cidades; Tempo ou combustível na distribuição de mercadoria;

    
def encontrar_subconjuntos(conjunto):
    subconjuntos = [[]]
    for elemento in conjunto:
        subconjuntos += [sub + [elemento] for sub in subconjuntos]
    return subconjuntos

conjunto = [1, 2, 3]
print(encontrar_subconjuntos(conjunto))
# Saída: [[], [1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3]]
        
    

Algoritmo guloso (greedy): É usado em problemas de otimização, onde se escolha a melhor opção em dado momento com a esperança de sua validade global. Nem sempre conduz à soluções ótimas globalmente e podem ter cálculos repetitivos. Deve-se definir a função de otimização do que é mais “apetitoso” e executá-la em cada iteração. Essa técnica não olha além da iteração atual, cada escolha é definitiva. Problemas: Máximal e minimal, otimização combinatórias.

    
def encontrar_troco_moedas(troco, moedas):
    moedas.sort(reverse=True)
    resultado = []
    for moeda in moedas:
        while troco >= moeda:
            resultado.append(moeda)
            troco -= moeda
    return resultado

moedas_disponiveis = [1, 5, 10, 25]
troco = 47
print(encontrar_troco_moedas(troco, moedas_disponiveis))
# Saída: [25, 10, 10, 1, 1]
    
    

Dividir e conquistar: Consiste em dividir o problema inicial em subproblemas menores, até que possam ser resolvidos diretamente. Depois combina-se os resultados para obter a solução final. Problemas: Merge sort; transformada discreta de Fourier; Torre de Hanói.

    
def merge_sort(lista):
    if len(lista) <= 1:
        return lista

    meio = len(lista) // 2
    esquerda = merge_sort(lista[:meio])
    direita = merge_sort(lista[meio:])

    return merge(esquerda, direita)

def merge(esquerda, direita):
    resultado = []
    i = j = 0

    while i < len(esquerda) and j < len(direita):
        if esquerda[i] < direita[j]:
            resultado.append(esquerda[i])
            i += 1
        else:
            resultado.append(direita[j])
            j += 1

    resultado.extend(esquerda[i:])
    resultado.extend(direita[j:])
    return resultado

lista = [9, 3, 7, 2, 1, 5, 6]
print(merge_sort(lista))  # Saída: [1, 2, 3, 5, 6, 7, 9]
    
    

Backtracking: É uma técnica de criar permutações de um subconjunto para então adicionar novos itens e analisámos como solução do problema. Caso não seja, apagar o adicionado e tentar outro. Deve-se guardar cada tentativa. É eficiente em problemas com espaço de busca grande e pode ser implementado de forma recursiva. Problemas: Oito rainhas, passeio do cavalo, jantar dos filósofos.

    
def permutacoes(lista):
    resultado = []
    backtrack(lista, [], resultado)
    return resultado

def backtrack(lista, caminho, resultado):
    if not lista:
        resultado.append(caminho)
        return

    for i in range(len(lista)):
        elemento = lista[i]
        novos_elementos = lista[:i] + lista[i+1:]
        backtrack(novos_elementos, caminho + [elemento], resultado)

lista = [1, 2, 3]
print(permutacoes(lista))
# Saída: [[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]

    

Heurísticas: São métodos que não garantem a melhor solução do problema, sendo a aproximação um caso particular. Não é possível provar formalmente sua qualidade ou convergência, são regras para levar a solução sem se saber exatamente como ocorreu. No caso aproximado podemos convergir o resultado até um limite desejado, nos heurísticos isso não acontece, mas medidos a complexidade média de obter a solução. A técnica exploratória é um tipo de busca cega, por um tipo de aproximação ao ponto ótimo definiado a priori.

    
def mochila_heuristica(pesos, valores, capacidade):
    n = len(pesos)
    proporcoes = [(valores[i] / pesos[i], pesos[i], valores[i]) for i in range(n)]
    proporcoes.sort(reverse=True)
    
    mochila = []
    peso_atual = 0
    valor_atual = 0
    
    for proporcao, peso, valor in proporcoes:
        if peso_atual + peso <= capacidade:
            mochila.append((peso, valor))
            peso_atual += peso
            valor_atual += valor
        else:
            proporcao_usada = (capacidade - peso_atual) / peso
            mochila.append((capacidade - peso_atual, proporcao_usada * valor))
            peso_atual = capacidade
            valor_atual += proporcao_usada * valor
            break

    return mochila, valor_atual

pesos = [2, 3, 5, 7, 9]
valores = [10, 5, 15, 7, 12]
capacidade_mochila = 20
print(mochila_heuristica(pesos, valores, capacidade_mochila))

    

Referências:

1. Desenvolvimento de Algoritmos - Rosely Sanches e Simone Senger de Souza
2. Projeto de Algoritmo - Paulo Feofiloff
3. Processamento de Cadeias de Caracteres
4. Garbage collection algorithms

< 8 - Análise de Algoritmos > 10 - Arquitetura e Organização de Computadores